1 Prog_Intro:
Einführung in die Programmierung von Computern
1.1 Wie alles begann...
1.1.1 v.u.Zt., Erfindung der Schrift
|

Tontafel
aus dem Zweistromland, ca 3000 Jahre alt.
|

Kernspeicher
(große Platine) mit 4 KB Speicherkapazität, 1973 vs USB
Stick mit 8 GB, 2009
|
Bereits die ersten menschlichen Kulturen
produzierten soviel Daten, das Hilfsmittel für die Aufbewahrung
und Verarbeitung dieser entwickelt werden mussten. Als Erfinder der
Schrift gelten die Sumerer, welche vor ca. 5000 Jahren im Stadtstaat
Uruk im Süden des heutigen Iraks lebten. Sie "speicherten"
ihre Daten auf Tontafeln. Wie sich herausstellte, eine äußerst
robuste und extrem dauerhafte Form!
Inhalt dieser ersten Schriftdokumente waren
Aufzeichnungen wirtschaftlicher Transaktionen wie etwa "Bauer X
lieferte n Scheffel Korn". Dies führte zur These, dass die
Schrift hauptsächlich entwickelt wurde als Verwaltungsinstrument
zur Beherrschung einer immer komplexeren Wirtschaft.
1.1.2 Jh. Dezimalzahlensystem
Eine wesentliche Grundlage des Rechnens sind
Zahlensysteme mit deren Hilfe Zahlen durch Zeichen bzw. Zeichenreihen
dargestellt werden. Die ersten additiven Zahlensysteme entstanden vor
etwa 5000 Jahren und das bekannteste ist das Römische
Zahlensystem.

Zwischen
dem 5. und 9. Jahrhundert unserer Zeitrechnung entstandene
Hindu-Arabische Zahlensystem (Dezimalsystem). Die 0 als neutrales
Element der Addition ist eine Erfindung indischer Mathematiker im 5
Jh. u. Z..
Die Araber vereinten die 0 mit neun arabischen
Ziffernsymbolen 1, 2, ..., 9 zum Dezimalsystem. Dieses ermöglicht,
komplizierte Rechnungen in einfache, -ziffernweise Rechenschritte zu
zerlegen. Das Rechnen wurde einfacher, und die Kunst des Rechnens
breitete sich in allen Bereichen der Wirtschaft und Wissenschaften
aus. Das Morgenland wurde zum kulturellen Zentrum der Welt.
1.1.3 16
Jh. Logarithmen und Rechenstab
Mit der
Renaissance beendete Europa die Stagnation und Rückständigkeit
auf dem Gebiet der Kultur und Wissenschaften. Astronomen blickten
neugierig in den Himmel, vermaßen den Lauf der Gestirne und
hatten plötzlich komplexe himmelsmechanische Aufgaben zu lösen.
Die gewaltigen
Dimensionen des Himmels ließen sich platzsparend in der
Exponentialschreibweise
von
Zahlenwerten ausdrücken. Dabei wird
jede
Zahl z als Potenz p zu einer Basis b dargestellt: z = bp.
Ein weiterer Vorteil dieser Zahlendarstellung ist, dass
Multiplikationen und Divisionen auf Addition und Subtraktion
zurückgeführt werden können: z1*z2 = bp1*
bp2
= bp1+p2.
Wenn die Basis b festgelegt wird,
dann kann eine Liste als Rechenhilfsmittel für Multiplikation
und Division erstellt werden, die zu jeder Zahl z den Exponenten p
zur Basis b liefert. Der Exponent p wird auch Logarithmus
log(z), und die Liste
Logarithmentafel
genannt.

Der
schottischen Lord NAPIER (oder auch NEPER, 1550-1617) gab 1614
vierstellige Logarithmentafeln heraus. NAPIER hat etwa 30 Jahre
seines Lebens zur Berechnung dieser Tafeln benötigt - ein
moderner Personalcomputer (PC) macht es in wenigen Sekunden!
Der englische
Astronom und Mathematiker Edmund GUNTER (1569/1581-1626) entwickelte
im Jahre 1624 das "Logarithmenlineal", einem direkten
Vorläufer des Rechenstabes. Seth PATRIDGE hat um das Jahr 1650
dem Rechenstab die uns bekannte Form gegeben.
1.1.4 17
Jh., erste mechanische Rechenmaschinen
Im 17.
Jahrhundert begannen mehrere Wissenschaftler mit dem Bau von
mechanischen Rechenmaschinen.
Der Tübinger
Professor der Astronomie und biblischer Sprachen, Wilhelm SCHICKARD
(1592-1635), entwickelte 1623 die erste Vierspeziesrechenmaschine für
die Grundrechenarten (+,-,*,/). Es existiert keine von ihm gebaute
Maschine mehr. Die Konstruktionsbeschreibung der Maschine ist in
einem Brief an KEPLER enthalten. Ein funktionierender Nachbau ist im
Deutschen Museum in München zu besichtigen.
Der
französische Mathematiker und Theologe Blaise PASCAL (1623-1662)
baute mit 19 Jahren eine Addiermaschine für 6-stellige Zahlen.
Pascals Vater
war Finanzbeamter. Das mühselige Rechenwerk des Vaters
motivierte den Sohn zu Konstruktion und Bau der Rechenmaschine.
PASCALs Maschine kann heute im Mathematisch-physikalischen Salon im
Dresdener Zwinger bewundert werden.
1.1.5 18
Jh., Dualzahlensystem
Der Mensch hat
zehn Finger, und die dienten wohl als erste Rechenhilfe. Nicht
verwunderlich, dass auch unser arabisches Zahlensystem im Zehnertakt
arbeitet. Aber es geht auch anders.
Der deutsche
Mathematiker Gottfried Wilhelm LEIBNIZ (1646-1716) entdeckte, dass
ein Zahlensystem nur mit den zwei Ziffern 0 und 1 aufgebaut werden
kann. Die minimale Ziffernzahl bewirkt auch einfachste Rechenregeln.
Leibniz war ein Genie. Das die simplen Rechenregeln der Dualzahlen zu
vereinfachten Konstruktionen für Rechenmaschinen führen
mussten, erkannte er. Und konstruierte die erste, mit Dualzahlen
arbeitende Rechenmaschine. Zur Serienfertigung mechanischer
Vierspeziesrechenmaschinen kam es erst Ende des 18. Jahrhunderts. Ein
Hersteller war der deutsche Pfarrer HAHN (1735-1790).
1.1.6 19
Jh., Rechnen mit Dampfkraft
Eine neue
Stufe in der Entwicklung der Rechentechnik und Datenverarbeitung
erkolmm Charles BABBAGE (1792-1871) mit der Konzeption der
programmgesteuerten
Rechenmaschine. Der
zwanzigjährige BABBAGE hatte 1812 mit seinem Freund HERSCHEL -
Astronom - Rechnungen zu prüfen, die für die Astronomical
Society gemacht worden waren. Immer wieder wurden von ihnen Fehler
entdeckt. "Ich wollte es ginge mit Dampf!" soll BABBAGE
gestöhnt haben. HERSCHEL soll geantwortet haben: "Das ist
gut möglich!". Diese so selbstverständlich gegebene
Antwort ließ BABBAGE nicht mehr zur Ruhe kommen. So kam er auf
die Idee, zwei zu diesem Zeitpunkt bekannte Einrichtungen
zusammenzuführen. Dies waren die Vierspeziesrechenmaschine und
der Steuermechanismus automatischer Webstühle mit Hilfe von
Lochkarten, der von Joseph-Marie JACQUARD (1752-1834) im Jahre 1808
entwickelt wurde.
BABBAGE hat seine Maschine nicht zu Ende bauen
können. Die Zeit war noch nicht reif dafür, die Mechanik
war teuer und unzuverlässig. Der fertiggestellte Teil seiner
imposanten Maschine kann heute im British Museum of Science in
Kensington (Stadtteil von London) besichtigt werden. Als BABBAGE 1871
als verkanntes Genie starb, hinterließ er uns neben seiner
"Unvollendeten" die im Groben noch heute gültige
Grundidee vom Aufbau eines modernen Rechners, der aus:
einem Speicher (store, für 1000 Zahlen
mit 50 Stellen)
einem Rechenwerk (mill)
einem Steuerwerk (control)
einer Eingabe- und Ausgabeeinheit
(input/output)
besteht.
1.1.7 1936,
Begründung der Berechenbarkeit mittels Turingmaschine
Alan Turing
konzipierte das Modell einer sehr einfachen Maschine, welche
prinzipiell alle berechenbaren Problemlösungen berechnen konnte.
Diese besteht aus einem unendliche langen Band als Speicher, einem
speziellen Schreib- Lesekopf und einem endlichen Automaten. Der vom
Band eingelesene Wert bewirkt ein Zustandsänderung im endlichen
Automaten. Mit jedem Zustandsübergang können
Vorwärts/Rückwärtsbewegungen des Kopfes, sowie
Schreibbefehle (Ausgabe auf dem Band) verbunden sein.
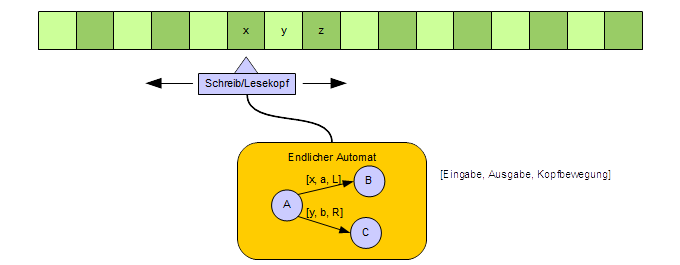
Die
Turingmaschine bildet eine wesentliche Säule der
Computertechnik.
1.1.8 1943,
Enschlüsseln von Funksprüchen mittels Colossus
In England
wird der Spezialrechner »Colossus« zur Unterstützung
beim Entschlüsseln von codierten Funksprüchen der deutschen
Wehrmacht eingesetzt.
1.1.9 1944, im Wohnzimmer entsteht aus
Dosenblech ein Computer
Der Bauingenieur Konrad ZUSE griff im Jahre 1935
die Ideen von BABBAGE wieder auf. Der Aufwand statischer Berechnungen
motivierte ZUSE. Aus Dosenblechen und Elektroschrott entstand im
Berliner Wohnzimmer der Eltern die Z1, der erste Computer nach
BABBAGE.
1.1.10 1944,
Computer berechnen nukleare Sprengsätze
In den USA
wird im Rahmen der Atombombenentwicklung der Computer MARK I
(Relaistechnik) zur maschinellen Lösung von
Differentialgleichungen aus der Teilchenphysik gebaut.
1.1.11 1946,
ENIAC das Röhrenmonster
In den USA
wird der Computer ENIAC mit 18000 Elektronenröhren als
Schaltelemente in Betrieb genommen.
1.1.12 1946,
Neumanns Minimalismus
Der ungarische
Mathematiker John von Neumann entwickelt eine Computerarchitektur,
die bei minimalen Hardwareeinsatz ein Maximum an Funktionalität
bietet.
1.1.13 1947,
Erfindung des Transistors
In den Bell-
Laboratorien (USA) wird der erste Transistor erfunden.
1.1.14 1958,
erster Mikrochip
Jack Kilby
(Fa. Texas Instruments) fertigt die erste integrierte Schaltung.
1.1.15 1964,
Evolution statt Revolution
IBM führt
das Großrechnersystem System/360 ein. Alle Nachfolger der Linie
360 sind zum System 360 abwärtskompatibel. D.h., Software, die
für ein 360er entwickelt wurde, kann z.B. auch auf einer 370er
ausgeführt werden. Dieses Prinzip fand großen Anklang bei
den Kunden. IBM wurde zum Marktführer in den 70'er Jahren.
1.1.16 1971,
erster Mikroprozessor
Die US Firma
INTEL entwickelt einen integrierte Schaltung, die eine komplette
Zentraleinheit umfasst. Der Chip erhält die Nummer 4004. Er ist
der Urahn aller heutigen x86 CPU's.
|
Programmierbarer Taschenrechner der Fa.
Comodore, ca. 1978

|
1.1.17 1975,
erste Homecomputer
In Amerikas
Garagen wird an der Zukunft gebastelt. Es entstehen die ersten
Funktionsmodelle von Homecomputern. Steve Jobs und Bill Gates gehören
zu den Homecomputer - Pionieren.
1980,
IBM präsentiert PC
Nach einer
geschäftlich sehr erfolgreichen Dekade dank Marktführerschaft
bricht plötzlich bei IBM Panik aus: Garagenschrauber wildern mit
Eigenbau- Homecomputer in IBM's Domäne, dem US Computermarkt.
In aller Eile
wird ein eigener Homecomputer zusammengebastelt, CPU (INTEL) und
Betriebssystem MS DOS (Microsoft) kauft man ein. Das Kind hört
auf dem Namen PC und soll den Vormarsch der Homecomputer stoppen.
Der PC wird
von der Kundschaft dankbar angenommen, es entwickelt sich ein
regelrechter PC- Markt. IBM ist der Dynamik dieses Marktes nicht
gewachsen und verliert schließlich trotz technologischem
Vorsprungs die Marktführerschaft. Die Zulieferer INTEL und
Microsoft steigen zu den neuen Marktführern auf.
1.1.18 1989,
vom ARPANET zum Internet
Das Ende des
kalten Krieges bewirkt, daß eine Reihe von Technologieen, die
hauptsächlich für militärische Zwecke bestimmt waren,
zur zivilen Nutzung freigegeben werden. So auch das 1969 in Betrieb
genommene ARPANET. Diese wurde als Atomschlagfestes militärisches
Kommunikationsmedium konzipiert. Aus dem ARPANET entwickelte sich
schließlich ein weltumspannendes Computernetzwerk, das
INTERNET.
1989 waren im
Internet 100000 Server online. Bis zum Jahr 1999 ist diese Zahl auf
über 56 Mio. Rechner weltweit angewachsen.
1.2 Warum programmieren ?
1.2.1 Mit Universalrechnern Probleme lösen
Unter Programmierung wird heute im wesentlichen
der Entwurf und die Implementierung von Algorithmen für sog.
Universalrechnern verstanden. Universalrechner sind Maschinen, die
theoretisch Lösungen von allen berechenbaren Problemen berechnen
können.
Im folgenden das Blockschaltbild eines
Universalrechners mit sog. Von Neumann - Architektur:
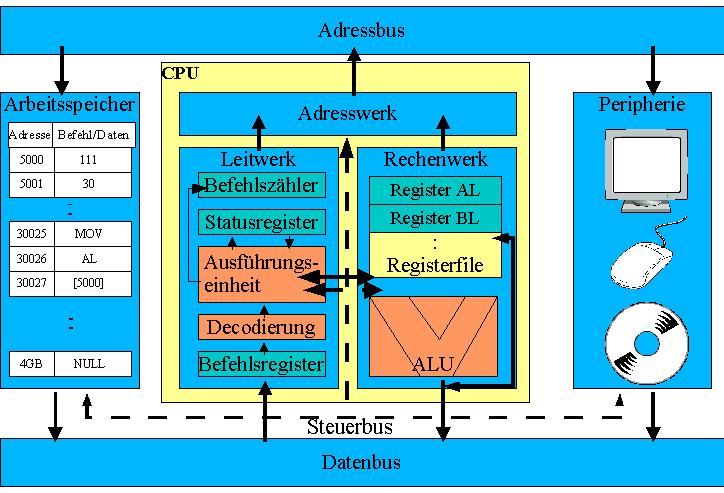
Die
moderne Welt von heute steuern Milliarden von Universalrechner-
integriert in die Geldkarte oder als Superrechner für die
Wettervorhersage. Für jedes berechenbare Problem kann der
Programmierer eine Lösung anbieten.
Im Detail können die Aufgabenstellungen für
Programmierer in folgende Bereiche aufgeschlüsselt werden:
1.2.2 Standardprogramme anpassen, Automatisierung
Standardprogramme sind z.B. Datenbankserver,
Office Suites wie MS Office oder Open Office, oder CAD- Programme wie
DS Catia oder AutoCad. Anwender benötigen oft spezielle
Anpassungen dieser Standardprogramme an ihre Geschäftslogik.
Z.B. sind spezieller Workflows abzubilden oder zusätzliche
Bibliotheken zu erstellen. Dieses Aufgabenfeld wird mit
Standardprogramme anpassen bezeichnet.
Der Programmierer muss die Schnittstellen der Standardprogramme
beherrschen. In der Regel diktieren die Schnittstellen der
Standardprogramme die Programmiersprache (z.B. für MS. Office
VBA, und für Catia VBScript).
1.2.3 Individualsoftware erstellen
Auf einer Plattform (PC oder Mikrocontroller) wird
eine völlig neue Anwendung erstellt. Der Programmierer kann die
Programmiersprache frei wählen. Theoretisch wird er eine
auswählen, mit der die Aufgabenstellungen und ihre Lösungen
besonders einfach abzubilden sind. Praktisch wird meist mit der
Programmiersprache die Implementierung der Lösung angegangen,
die dem Programmierer vertraut ist.
Eine gute Auswahl einer Programmiersprache für
eine Aufgabenstellung führt zu einer schnellen Fertigstellung
des Projektes und liefert einen sehr gut strukturierten Code, der
leicht wartbar ist.
1.3 Algorithmen und Programme
Computern berechnen Lösungen für
Probleme, indem sie Programme ausführen. Programme sind
computerlesbare Darstellungen von Algorithmen.
|
Definition
|
|
Algorithmus
|
»Ein Algorithmus ist ein mit 1)
endlich langem Text formuliertes, 2) schrittweises
Problemlösungsverfahren, wobei 3) jeder Schritt
(Aktion) für eine bestimmte Klasse von Prozessoren eindeutig
und ausführbar ist. Die Ausführung eines Schrittes kann
(muss aber nicht) eine Zustandsänderung von Objekten
bewirken und 4) schließt die Bestimmung der als
nächstes auszuführenden Aktion ein.« /Blaschek:
Einführung in die Programmierung mit Modula-2, Springer
Verlag Berlin Heidelberg 1987/
Eine weitere wichtige Eigenschaft von
Algorithmen, welche die obige Definition nicht erfasst, ist das
sie terminieren (nach
endlich vielen Schritten anhalten), wenn eine Lösung
errechnet/gefunden wurde.
|
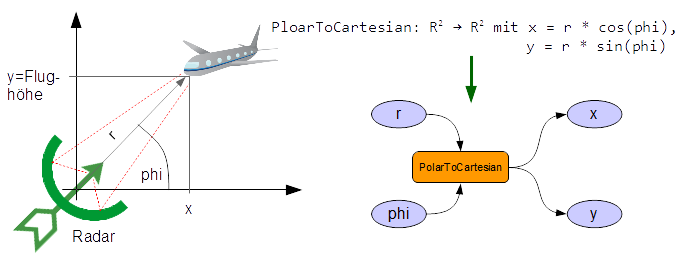
1.3.1 Algorithmen berechnen Funktionen
Ein Algorithmus ist im Allgemeinen eine
Berechnungsvorschrift für eine Funktion. Eine Funktion im
mathematischen Sinne bildet die Elemente einer Menge, auch
Definitionsbereich genannt, auf die einer anderen Menge, auch
Wertebereich genannt, ab.
f: D → W mit D <=>
Menge des Definitionsbereiches, W <=> Menge des Wertebereiches
Ein
Beispiel dafür ist die Umrechnung von Polarkoordinaten
(Drehwinkel + Abstand) in kartesische Koordinaten (x,y). Das
rotierende Flughafenradar erfasst z.B. die Position eines Flugzeugs
in Polarkoordinaten. Die umgerechnete y Koordinate entspricht der
Flughöhe.
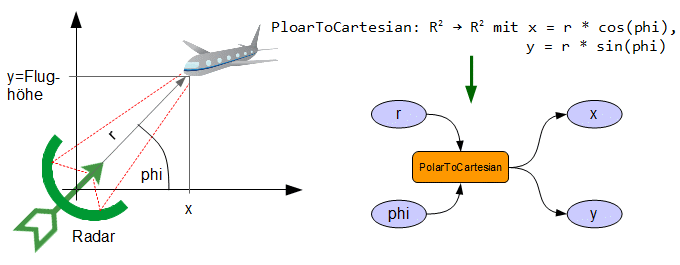
Aus
Sicht eines Algorithmus ist der Definitionsbereich die Menge der
möglichen Eingaben und
der Wertebereich die Menge der möglichen Ausgaben.
Definitionsbereich <=>
Menge der Eingaben,
Wertebereich <=> Menge
der Ausgaben
Diese Betrachtung führt zu einer
Grundstruktur der elektronischen Datenverarbeitung, der Eingabe →
Verarbeitung → Ausgabe Struktur, oder kurz EVA.
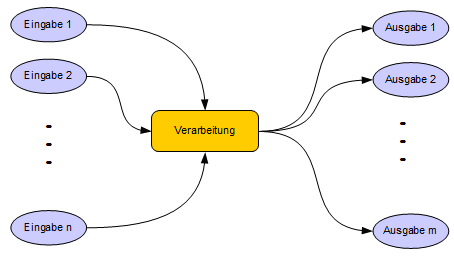
Wie
aus dem Bild zu sehen, bilden die Eingaben endliche n- Tupel, die
durch die Verarbeitungsfunktion = Algorithmus auf ein endliches m-
Tupel der Ausgabe abgebildet werden.
1.3.2 Entscheidungsverfahren
Berechnet eine Algorithmus eine Funktion, die
Eingaben auf eine der beiden Wahrheitswerte true oder
false abbildet, dann
wird dieser Entscheidungsverfahren genannt:
Algo_?:
E → B mit B:={true, false}
Beispiel: Algorithmus für eine Funktion, die
zwei für gegebene natürliche Zahlen n und t entscheidet, ob
t ganzer Teiler von n ist.
IstTeiler: NxN → B
mit (n,t) ϵ NxN, b ϵ
B:={true, false}
wobei (n,t) → true wenn
t Teiler von n, (n,t) → false sonst
Ein Berechnungsverfahren (Algorithmus) für
die Funktion ist folgendes
Wenn n = 0 ist, dann ist t ein Teiler von n.
Fertig!
Wenn n > 0 ist, dann berechne n = n-t und
mache weiter bei 1.
n ist kein Teiler. Fertig !
1.3.3 Abzählverfahren
Berechnet ein Algorithmus eine Funktion, die
Eingaben auf eine natürliche Zahl n abbilden, dann wird dieser
Abzählverfahren genannt:
Algo_#:
E → N mit N Menge der nat. Zahlen
Beispiel:
AnzMitTeiler5:
{2, 4, 8, 9, 11, 13, 15} → N
1.3.4 Algorithmen mit Programmiersprachen
implementieren
Ein Computer berechnet die Lösung einer
Aufgabe durch einen Algorithmus, indem er ein Programm ausführt.
Das Programm ist eine Darstellung eines Algorithmus in einer Form,
die der Computer lesen und verarbeiten kann. Die formalen Systeme,
mit denen computerlesbare Formate von Algorithmen erstellt werden
(=Programme) werden als Programmiersprachen bezeichnet.
Die Formulierung eines Algorithmus in einer
Programmiersprache wird auch als Implementierung bezeichnet.
1.3.4.1 FUNC: Programmieren mit Funktionen
Die Mathematiker entwickelten in Jahrhunderten
eine eigene Sprache: die Sprache der Formeln und Funktionen. Diese
Sprache besteht aus Operatoren wie z.B. + und *, Zahlendarstellungen
und Symbolen für Konstanten (z.B. π)
und Veränderliche
(z.B. x, D). Beispiele sind die Formel zur Berechnung des
Kreisumfanges:
U = π * D
1.3.4.1.1 Funktionen
Allgemeiner kann man den Zusammenhang zwischen
Durchmesser D eines Kreises und seinem Umfang U durch eine Funktion
darstellen:
f(D): D → π * D
Den Ausdruck kann man lesen als: die Funktion f(D)
ordnet jedem Durchmesser D einen Kreisumfang f(D) =
π
* D zu. Diese Darstellung wurde in den 1930-er Jahren zu einem
präzisen Formalismus ausgearbeitet (Alonzo Church, Stephen
Kleene: Lambda- Kalkül), welcher die Grundlage für die
Familie der funktionalen
Programmiersprachen
wie z.B. LISP oder F# bildet.
Während
die Mathematiker Funktionen gerne mit einem einzigen Buchstaben
bezeichnen, und dabei auch noch auf das griechische Alphabet
zugreifen, bevorzugen die Programmierer lieber sprechende Namen wie:
Kreisumfang(D):
D → π * D
1.3.4.1.2 Fallunterscheidungen
Neben
den Ausdrücken wie
π
* D
können
die Abbilder von Funktionen auch durch Fallunterscheidungen definiert
werden. Z.B. kann die Funktion, die jeder Zahl ihren absoluten Betrag
zuordnet, wie folgt beschrieben werden:
Fallunterscheidungen
-z z < 0
|z| = Abs(z): z → 0 für z = 0
z z > 0
z.B. Abs(-5) = 5, Abs(5) = 5, Abs(0) = 0
1.3.4.1.3 Funktionen
hintereinander schalten, Komposition
In
der Mathematik kann man mittels Funktionen eine Menge {x} auf eine
Menge {y}, und die Menge {y} wiederum auf die Menge {z} abbilden.
Formal wird dies wie folgt beschrieben:
Wenn
f1(x): x → y und f2(y): y → z dann ist
f2(f1(x))
: x →
z
Damit
kann man z.B. die Berechnungen des Kreisumfanges an Durchmesser
anpassen, die in verschiedenen Maßeinheiten gemessen wurden:
Funktionen hintereinanderschalten
MillimeterInMeter(x): x → x * 0,001
CentimeterInMeter(x): x → x * 0,01
Kreisumfang(D): D → π * D
D D
/--------+--------\ /----+----\
Kreisumfang(MillimeterInMeter(x)): x → π * (x * 0,001)
Kreisumfang(CentimeterInMeter(x)): x → π * (x * 0,01)
z.B. Kreisumfang(CentimeterInMeter(100)) = 3,142..., Kreisumfang(MillimeterInMeter(100)) = 0,3142...
1.3.4.1.4 Rekursion
Mathematiker
sind findige Menschen. Sie hatten schnell erkannt, dass mit der
Hintereinaderschaltung von Funktionen ein mächtiges Instrument
bereitsteht, mit dem man sich weit in die Tiefen mathematischer
Probleme vorwagen kann. Eine besondere Form ist die Rekursion. Auf
dieser basieren die funktionalen Beschreibungen vieler mächtiger
Algorithmen.
Z.B.
soll ein Vertreter 3 Kunden nacheinander besuchen, wobei die gewählte
Reihenfolge die mit der kleinsten Gesamtstrecke ist (Problem der
Rundreise mit minimaler Streckenlänge).
Die
Lösung benötigt zunächst einen Graphen, dessen Knoten
den Startpunkt und die Kunden darstellen, und dessen Kanten die
Entfernungen zwischen den Knoten angeben. Dann sind für alle
möglichen Reihenfolgen der Besuche die Summen der Wege zu
berechnen. Am Ende ist die Reihenfolge mit der kleinsten Summe als
Lösung auszuwählen. Folgendes Bild veranschaulicht das
Vorgehen:
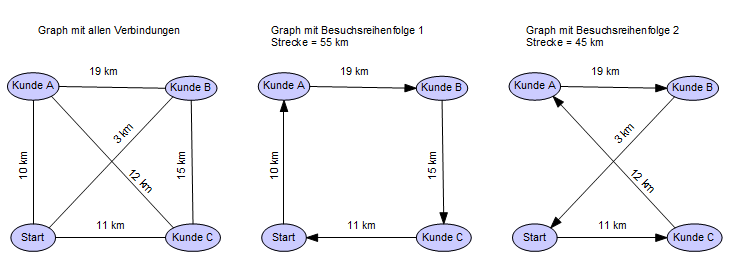
Wie
viele Reihenfolgen über dem Graphen, und wie viele Summen damit
gebildet werden müssen, gibt die aus der Kombinatorik bekannte
Fakultät-
Funktion
an:
Fakultät berechnen
1 n = 0
N!(n): n → für
n*N!(n-1) n > 0
Die
Funktion wird mittels einer Fallunterscheidung definiert, wobei für
den Fall n > 0 der Funktionswert durch einen Term beschrieben
wird, der N! wiederum enthält. Man erhält eine Lösung,
indem man auf eine Lösung für den Vorgänger
zurückgreift. Diese Art von Funktionsdefinition wird Rekursion
genannt.
Aufgelöst
wird die Rekursion von N! z.B. für n = 3 wie folgt:
N!(3) = 3*N!(2) = 3*2*N!(1) = 3*2*1*N!(0) = 3*2*1*1 = 6
Die
Fakultät wächst mit n extrem. Die exakte Lösung des
Rundreiseproblem für große n praktisch unmöglich.Übung
Implementiere
eine rekursive Funktion, die eine gegebene Zahlenpaar
Basis,
Exponent
die
Potenz berechnet wie folgt:
Potenz(Basis,
Exponent): (Basis, Exponent) → Basis
Exponent
Beachte
dabei die Beziehung: b
e
=
b * b
e-1
=
b * b * b
e-2
1.3.4.1.5 Listenverarbeitung
In
den Naturwissenschaften werden oft mehrere Messwerte einer
Beobachtung zugeordnet werden. Es entstehen Paare von Messwerten. Ein
Beispiel ist die Beobachtung eines beschleunigenden Fahrzeugs. Dabei
wird in festen Zeitabständen die Momentangeschwindigkeit
notiert.
Messung: {(v, t)} := {(1 m/s, 1s), (2 m/s, 2s), …, (12 m/s, 5s)}
Ein
anderes Beispiel sind die möglichen Folgen, in denen die Kunden
A, B, C besucht werden (siehe vorausgegangener Abschnitt)
Besuchsreihenfolgen: {(K1, K2, K3)} := {(A, B, C), (B, A, C), (B, C, A), (C, B, A), (C, A, B), (A, C, B)}
Die
Permutationen über der dreielementigen Menge {A, B, C} bilden
hier alle möglichen Reihenfolgen. Jede Reihenfolge wird als ein
Triple dargestellt.
Paare,
Tripel oder allgemein Tupel sind spezielle Formen von Listen.
Liste := (e1, e2, …., eN)
Mit
Listenverarbeitung werden allgemein Funktionen bezeichnet, die Listen
auf Listen oder Listen auf skalare Werte abbilden
Listenverarbeitung := {f mit f(Liste X) : Liste X → Liste Y oder f(Liste X): Liste X → Y}
Folgenden
Tabelle definiert die grundlegenden Funktionen der Listenverarbeitung
|
Name
|
Beispiel
|
Beschreibung
|
|
L(…):(x1,…,
xn) → {x1, …,xn}
|
L(1,2,3) →
{1, 2, 3}
|
Erzeugt eine Liste mit den angegebenen
Elementen.
|
|
IX({…},NN):({x1,…,
xi, … ,xn},(i)) → xi
|
IX(L(1,2,3),1)
→ 2
|
Liefert den Wert des i-ten Listenelementes
|
|
Count({…}):({x1,…,
xn})→ n
|
Count(L(1,2,3))
→ 3
|
Gibt die Anzahl der Elemente in einer Liste
zurück
|
|
First({…}):({x1,
… , xn}) → x1
|
First(L(1,2,3))
→ 1
|
Gibt das erste Element einer Liste zurück
|
|
Rest({…}): ({x1,
x2,…, xn}) → {x2,…,xn}
|
Rest(L(1,2,3)) → {2,
3}
|
|
|
Last({…}):
({x1, … , xn}) → xn
|
Last(L(1,2,3))
→ 3
|
Gibt das letzte Element einer Liste zurück.
|
|
Reverse({…}):({x1,
… , xn}) → {xn, … , x1}
|
Reverse(L(1,2,3))
→ {3,2,1}
|
Liefert eine Liste mit allen Elemente der
Eingangsliste in umgekehrter Reihenfolge
|
|
Take({…},
i)
|
Take(L(1,2,3,4),
2) → {1,2}
|
Liefert eine Liste mit den ersten i Elemente
der ursprünglichen Liste
|
|
Skip({…},
i)
|
Skip(L(1,2,3,4),
2) → {3,4}
|
Liefert eine Liste mit den ersten i Elemente
der ursprünglichen Liste
|
|
Concat({…},{…})
|
Concat(L(1,2,3),{4,5})
→ {1,2,3,4,5}
|
Verkettet zwei Listen zu einer neuen Liste
|
|
ForEach({…},
f)
|
ForEach(L(1,2,3),
λ(x)
x*x) → {1,2,3,4,5}
|
Liefert zu einer Liste die Liste mit den
Funktionswerten f(x) für jedes x aus der eingegebenen Liste.
|
1.3.4.1.6 Funktionen in C und C# implementieren
In der Gegenwart dominieren Programmiersprachen,
deren Syntax mit der Programmiersprache C verwandt sind. Im folgenden
Elemente aus C, um Funktionen zu programmieren:
|
Pos
|
Sprachelement, Beispiel
|
Bedeutung
|
|
0
|
// Kommentar
|
Eine Zeile im Programm, die nicht als tron-
Befehl ausgewertet wird.
|
|
1
|
int
|
Definiert die Menge der ganzen Zahlen
|
|
2
|
int ADD(int a, int b){
return
a + b;
}
|
Definiert eine Funktion ADD, die zwei ganze
Zahlen a und b auf die Summe von a und b abbildet:
ADD: (a, b) → a+bZah
|
|
3
|
...(int a, int b)
|
Parameterliste einer Fuktion
|
|
4
|
...
{
return
a + b;
}
|
Funktionsrumpf oder Block einer Funktion
|
|
5
|
int ADD ...
|
Rückgabewert einer Funktion (vom Typ ganze
Zahl)
|
|
6
|
int AbsoluterBetrag(int
z) {
if(z
>= 0)
return
z;
else
return
-1*z;
}
|
Funktion, deren Funktionswert mittels einer
Fallunterscheidung bestimmt wird.
|
|
7
|
IEnumerable<int>
|
Menge von Listen ganzer Zahlen
|
|
8
|
Fn.L(2, 3, 5)
|
Funktion, die alle übergebenen Argumente
auf eine Liste abbildet
|
|
9
|
Fn.First(Fn.L(2, 3, 5))
|
Liefert das erste Listenelement (2)
|
|
10
|
Fn.Rest(Fn.L(2, 3, 5))
|
Liefert den Rest der Liste
|
1.3.4.1.7 Beispiele
zur funktionalen Programmierung
Im
Folgenden Beispiele für einfache Funktionen zur
Listenverarbeitung. Wie man sieht, wird die Rekursion intensiv
genutzt:
1.3.4.1.7.1 Bildet
die Summe aller Werte in einer Liste
Summenbildung
Summe({a1, a2, …, aN}): {a1, a2, …, aN} → a1 + a2 + … + aN
Function Summe(liste)
If Count(liste) = 0 Then
Return 0
ElseIf Count(liste) = 1 Then
Return liste(0)
Else
Return First(liste) + Summe(Skip(liste, 1))
End If
End Function
1.3.4.1.7.2 Minimum
einer Liste suchen
Minima finden
Min({…}): {…} → min mit min ϵ {…} & Für alle x ϵ {…} gilt: min <= x
Erzeugt
eine Liste mit den Werten 1-N:
Liste mit Werten erzeugen
PTupelStart(n): n → {1,2, …,n}
Function PTupelStart(n)
If n = 1 Then
Return {1}
Else
Return Concat(PTupelStart(n - 1), {n})
End If
End Function
1.3.4.1.7.3 Zwei
Listen auf Identität prüfen
Gleichheit von Listen prüfen
Equal({a1,a2,…,aN}, {b1,b2,…,bM}): ({a1, a2, …, aN}, {b1, b2, …, bM}) → true für
Count({a1,a2,…,aN}) = Count({b1, b2, …, bM}) und
1.3.4.1.7.4 IstTeiler
1.3.4.1.7.5 Zähle alle mit Teiler t
AnzMitTeiler5:
{2, 4, 8, 9, 11, 13, 15} → N
public int ZähleAlleMitTeiler(IEnumerable<int> Liste, int t)
{
if(Fn.Count(Liste) > 0) {
if (IstTeiler(Fn.First(Liste), t))
return 1 + ZähleAlleMitTeiler(Fn.Rest(Liste), t);
else
return ZähleAlleMitTeiler(Fn.Rest(Liste), t);
} else return 0;
}
1.3.4.1.7.6 Algorithmus zum addieren von Dualzahlen
Ein Beispiel
für einen Algorithmus ist die Addition von Dualzahlen. Im
Folgenden wird die Addition zwei einstelliger Dualzahlen als
Funktion, und die Implementierung durch einen EVA- Graph aus
einstelligen Addieren dargestellt.
Ein
einstelliger Addierer bildet die Summe aus zwei Dualzahlen, die nur
aus einer einzigen Stelle bestehen, z.B:
R = 0 + 0, oder R = 1 + 0, oder R = 0 + 1, oder R = 1 + 1
Der einstellige Addierer
berücksichtigt einen Übertrag aus einer vorausgegangenen
einstelligen Addition, und gibt neben der Summe zusätzlich einen
möglichen Übertrag aus.
Im
Folgenden Bild ist der einstellige Addierer als Funktion, als EVA-
Graph und die Berechnung der Funktion als Entscheidungsbaum
dargestellt.
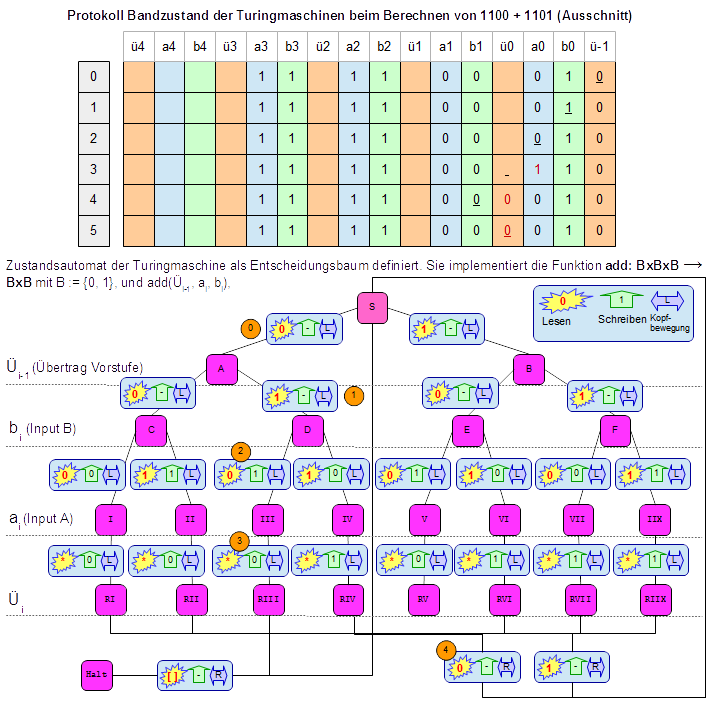
Aus
einen gegebenen Tripel von Eingaben (Ü
i-1
,
b
i
,
a
i
)
wird das Wertepaar (R
i
,
U
i
)
mittels Entscheidungsbaum berechnet, indem ausgehend von Knoten S
zuerst Üi-1 betrachtet: ist Üi-1 = 0, dann weiter bei
Knoten A, sonst bei B. Danach wird bi betrachtet. War Ü
i-1
= 0, und ist bi
= 1, dann weiter bei Knoten D. Wenn
Ui -1 =
0, bi =
1, und ai =
1 sind, dann kommt man in Knoten IV an. Unter dem Baum steht eine
Tabelle. Aus dieser kann das Ergebnis für Ri
und Ui
abgelesen werden. Für den
Knoten IV lautet das Ergebnis Ri
= 0, Ui
= 1.
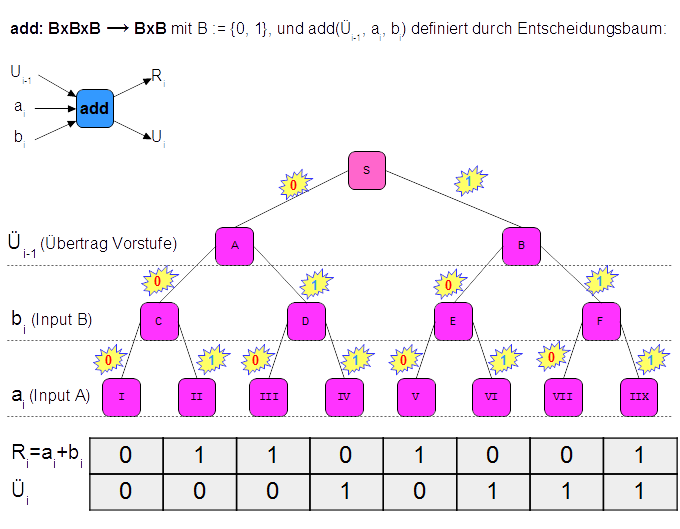
Aus
dem EVA - Graph des einstelligen Dualzahl - Addierer kann durch
Hintereinanderschaltung ein Addierer für mehrstellige Dualzahlen
gewonnen werden:
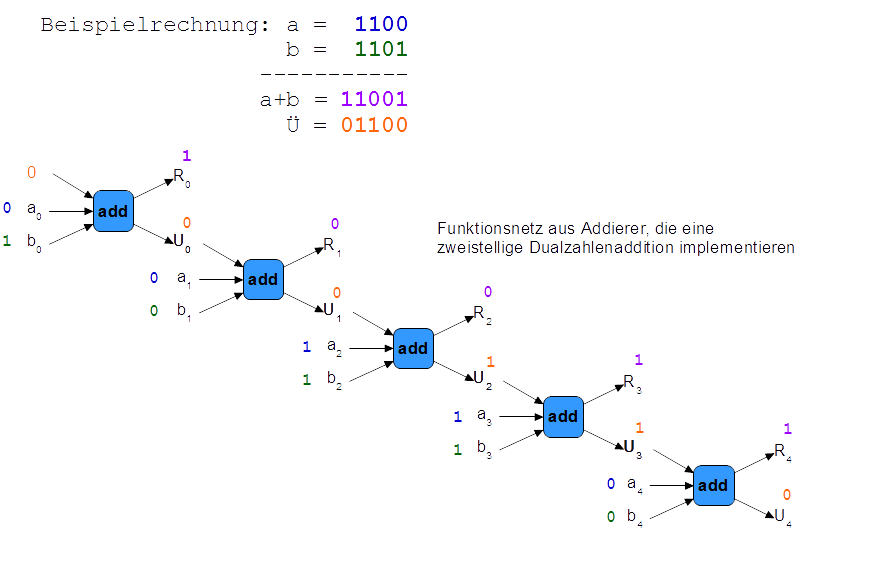
Diese
graphisch dargestellte Verkettung der Addierer Funktionen wird in der
Mathematik
Komposition
genannt.
Die Komposition zweier Funktionen ist wie folgt definiert:
g:
X → Y und h: Y → Z, dann ist die Komposition k = g
◦
h:
X → Z mit g
◦
h
:= h(g(x))
Die
add: (Ü
i-1
,
a
i
,
b
i
)
→ (Ü
i
,
R
i
)
Funktion bildet ein Tripel auf ein Wertepaar ab. Bei der Komposition
der Addierer ist aber nur der erste Teil des Wertepaares vom Bild als
Eingang für die nächste Addierstufe einzusetzen. Auch
hierfür bietet die formale Sprache der Funktionen eine Lösung,
die
Projektion der k-ten Komponente eines n- Tupels
:
p_k:
M
1
x
… x M
n
→
M
k
mit 1
≤
k
≤
n
und p_k(m
1
,
… ,m
n
)
= m
k
Somit kann man
zwei Addierer wie folgt formal kombinieren, um die zweite Stelle und
den 2. Übertrag zu berechnen
(Ü1, R1) := add(p_0(add(0, a0, b0)), a1, b1)
Ein Tupel, das die Summe aus zwei
zweistelligen Dualzahlen darstellt, kann nun definiert werden durch:
add2(a1, a0, b1, b0):=(p_0(add(p_0(add(0, a0, b0)), a1, b1)), p_1(add(p_0(add(0, a0, b0)), a1, b1)) , p_1(add(0, a0, b0))
Die erste Komponente des
Ergebnistupels ist der mögliche Übertrag, der bei der
Berechnung der 3. Stelle einfließt.
1.3.4.2 TRON: Programmieren mit Befehlen
Eine Programmiersprache kann die Funktionen und
Funktionsgruppen der Hardware direkt abbilden. Als Beispiel diene ein
vereinfachtes, virtuelles (<=> nicht real existierendes)
Rechensystem mit dem "Künstlernamen" TRON. Im
folgenden sein Aufbau als Blockschaltbild:
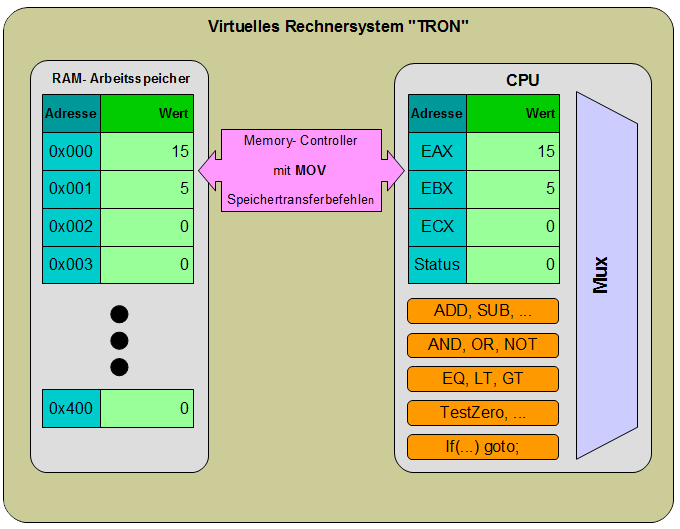
TRON
besteht aus:
einem Arbeitsspeicher (RAM)
einer CPU mit Registerfile und darauf
operierenden Schaltwerken, die Grundrechenarten wie Addition,
logische Operatoren wie AND, und Sprungbefehle implementieren
einem Memeorycontroller, der
Speichertransferbefehle anbietet, um Daten zwischen RAM und
Registerfile der CPU auszutauschen
Die Baugruppen von TRON können mit sehr
einfachen Befehlen angesteuert werden. Die Menge all dieser Befehle
von TRON wird als Maschinensprache von
TRON bezeichnet, und ist ein Beispiel einer simplen, imperativen
Programmiersprache:
|
Pos
|
Sprachelement, Beispiel
|
Beschreibung
|
|
1
|
var tron =
TRON.Computer.V1
|
Zugriff auf den TRON- Computer über Symbol
tron einstellen
|
|
2
|
CPU.Register.EAX
|
Adresse des Registers EAX
|
|
3
|
RAM.Address.C(99)
|
Adresse der Speicherzelle 100 im RAM
(Adressierung beginnt mit 0)
|
|
4
|
var Z = CPU.Register.EAX
|
Aliasname für Adresse EAX durch binden
dieser an das Symbol Z vergeben
|
|
5
|
tron.MOV(CPU.Register.EAX,
RAM.Address.C(99))
|
32 bit Wert aus der Speicherzelle 99 im RAM
wird in das Register EAX in der CPU kopiert
|
|
6
|
tron.MOV(RAM.Address.C(99),
CPU.Register.EAX)
|
32 bit Wert aus dem Register EAX in der CPU
wird in die Speicherzelle 99 kopiert.
|
|
7
|
tron.ADD(CPU.Register.EAX,
CPU.Register.EBX)
|
Werte aus EAX und EBX werden addiert. Das
Ergebnis wird in EAX zurückgeschrieben.
|
|
8
|
tron.EQ(CPU.Register.EAX,
CPU.Register.EBX)
|
EAX wird mit EBX verglichen. Wenn gleich, dann
wird das TestZero- Flag im Statusregister gesetzt
|
|
9
|
tron.cpu.TestZero
|
Ist true, wenn das Zero- Flag im Statusregister
gesetzt wurde, sonst false
|
|
10
|
goto SPRUNGMARKE;
|
Sprungbefehl: Es wird mit den Befehlen, die
sich unmittelbar hinter der Sprungmarke befinden, fortgesetzt.
|
|
11
|
if(tron.cpu.TestZero)
goto SPRUNGMARKE;
|
Bedingter Sprungbefehl: Nur wenn die Bedingung
(hier TestZero) true liefert, dann wird mit den Befehlen nach der
Sprungmarke fortgesetzt. Sonst wird nach diesem Befehl
fortgesetzt.
|
1.3.4.2.1 Beispiele
1.3.4.2.1.1 IstTeiler
Beispiel: Algorithmus für eine Funktion, die
zwei für gegebene natürliche Zahlen n und t entscheidet, ob
t ganzer Teiler von n ist.
IstTeiler: NxN → B
mit (n,t) ϵ NxN, b ϵ
B:={true, false}
wobei (n,t) → true wenn
t Teiler von n, (n,t) → false sonst
Ein Berechnungsverfahren (Algorithmus) für
die Funktion ist folgendes
Wenn n = 0 ist, dann ist t ein Teiler von n.
Fertig!
Wenn n > 0 ist, dann berechne n = n-t und
mache weiter bei 1.
n ist kein Teiler. Fertig !
Das Brechungsverfahren kann z.B. auf TRON
programmiert werden:
public static bool IsTeiler(int z, int t)
{
// Symbole binden
var tron = TRON.Computer.V1;
var Z = CPU.Register.EAX;
var T = CPU.Register.EBX;
var Zero = CPU.Register.ECX;
// Daten in die Register laden
tron.MOV(Z, AbsoluterBetrag(z));
tron.MOV(T, t);
tron.MOV(Zero, 0);
ANFANG:
// 1. Ist z = 0, dann ist t ein Teiler
if(tron.EQ(Z, Zero)) return true;
// 2. Wenn z < 0, dann ist t kein Teiler
if(tron.LT(Z, Zero)) return false;
// 3. z = z - t
tron.SUB(Z, T);
goto ANFANG;
}
Die Funktion kann mittels FUNC
wie folgt implementiert werden:
public int ZähleAlleMitTeiler(IEnumerable<int> Liste, int t)
{
if(Fn.Count(Liste) > 0) {
if (IstTeiler(Fn.First(Liste), t))
return 1 + ZähleAlleMitTeiler(Fn.Rest(Liste), t);
else
return ZähleAlleMitTeiler(Fn.Rest(Liste), t);
} else return 0;
}
1.3.5 Theoretisches Fundament der
Programmierung
1.3.5.1 Algorithmen mit primitiv rekursiven Funktionen
implementieren
Das Beispiel
des Dualzahl - Addierer skizziert, wie Algorithmen durch funktionale
Abbildungen beschrieben werden können. Dabei werden einfache
Abbildungen durch
Komposition
und Projektion
zu komplexen Abbildungen
kombiniert. 1926 vermutete David
Hilbert, dass jede
berechenbare, und damit durch einen Algorithmus beschreibbare
Funktion, einer sogenannte Primitiv
rekursive Funktion "entsprechen"
muss. Primitiv rekursive Funktionen sind eine Teilmenge von
Funktionen auf natürlichen Zahlen der Art
Pr:
N
k
→
N
mit N :=
Menge der natürlichen Zahlen
Sie
dienen den theoretischen Informatikern als
Stellvertreter/Abstraktionen für Aufgaben aus der Praxis. Die
natürlichen Zahlen vertreten dabei die "realen"
Eingaben (sie nummerieren sie durch) und Ergebnisse von Programmen.
Das Abbilden realer Probleme auf Funktionen natürlicher Zahlen
wird auch
Gödelisierung
genannt.
Folgende
Grundfunktionen gelten als primitiv rekursiv:
Nullfunktionen
0k:
Nk
→ 0
=> Initialisierung
Projektionen
p_k: Nn
→ N
mit 1≤k≤n
und p_k(n1,
… ,nn)
= nk
=> Zugriff auf
Listenelement
Nachfolgerfunktionen
nf: N → N mit x ϵ N gilt nf(x) = x+1
=> Inkrement
Auf
diese Menge an Grundfunktionen können noch die Komposition und
primitive Rekursion
angewendet
werden, um komplexere Funktionen zu kombinieren.
Komposition
c: g1,…,gm:
Nk
→ N
und h:Nm
→ N,
dann ist c = g◦h:
Nk
→ N
mit g◦h
:= h(g1(n1,…,nk),…,gm(n1,…,nk))
=> Verschachtlung,
Klammerung
Primitive
Rekursion R: Nk
→ N,
g: Nk-1
→ N,
h: Nk+1
→ N
mit R(n1,
n2,…,
nk):=
g(n2,…,
nk)
für n1 = 0, h(R(n1-1,
n2,
… , nk),
n1-1,
n2,
… , nk)
sonst
=> Zähler
gesteuerte Schleife, wobei n1
der Zähler, n2,…,
nk die
Randbedingungen, g(n2,…,
nk)
der aus den Randbedingungen folgende Startwert für eine
Iteration ist, und h den eigentlichen Iterationsschritt darstellt
Hinter
dem => steht in den Definitionen eine intuitive Deutung für
denjenigen, der bereits Erfahrungen mit Programmiersprachen gesammelt
hat. Die Deutungen können mit der Berechenbarkeit primitiv
rekursiver Funktionen durch LOOP-
Programme begründet werden.
LOOP-
Programme bestehen aus Zählschleifen, Zuweisungen,
Additionen und Subtraktionen. Ein LOOP- Programm, das zwei Zahlen a
und b addiert, ist folgendes:
sum := a
LOOP b DO
sum := sum + 1
END
In der Zeile LOOP b DO wird b um
1 vermindert (dekrementiert). In der Zeile END hält das Programm
an, wenn b den Wert 0 hat. Sonst wird wieder in die Zeile LOOP b DO
zurückgesprungen.
Im
wesentlichen bestehen damit LOOP- Programme aus einer endlichen
Anzahl von Schritten, die im komplexesten Fall n mal wiederholt
werden können. Für LOOP- Programme kann damit die maximale
Anzahl der Schritte zur Berechnung der Lösung vorausgesagt
werden. Damit sind diese Art von Algorithmen einfach beherrschbar.
Kochrezepte
(einfache Folge von Schritten), oder die Berechnung eines
Näherungswertes für π über eine Reihe wie
Σ(-1)/(2n+1) (Zählschleife über m Reihenglieder) sind
Beispiele für Algorithmen, deren Struktur durch primitiv
Rekursive Funktionen beschreibbar ist.
1.3.5.2 μ
Rekursion
Die
Annahme, das die Struktur aller Algorithmen und damit berechenbaren
Funktionen im Kern den primitiv rekursiven Funktionen entspricht,
erwies sich jedoch als falsch:
Wilhelm
Ackermann
,
Schüler von Hilbert, fand ebenfalls im Jahr 1926 eine Funktion,
die nicht als primitiv rekursive Funktion darstellbar ist, dennoch
aber berechenbar war: die
Ackermannfunktion
.
Hier
eine vereinfachte Definition der Ackermannfunktion:
m,
n ϵ N
ack(0,
m) = m+1
ack(n+1,
0) = a(n, 1)
ack(n+1,
m+1) = a(n, ack(n+1, m))
Diese Funktion
hat die Eigenschaft, Werte in Größenordnungen aus kleinen
Eingaben zu errechnen und dabei Rekursionstiefen zu erreichen, deren
Ausmaß jede primitiv rekursiven Berechnung weit übersteigt.
Der Wert ack(4, 4) ist schon größer als die theoretische
Anzahl aller Atome im Universum !
ack(0, 0) = 1, ack(1, 1) =
3, ack(2, 2) = 7, ack(3, 3) = 61, ack(4, 4) > #Atome im All
Die "wilde"
Rekursion der Ackermannfunktion, deren Schrittzahl/Rekursionstiefe
pro Berechnung nicht aus den Eingaben abschätzbar ist, kann
nicht in das Schema der primitiv rekursiven Funktionen gequetscht
werden. Dennoch ist sie berechenbar, wie die Definition, die nichts
weniger als ein Algorithmus ist, beweist !
Primitiv
Rekursive Funktionen sind damit nicht ausreichend als Bausteine zur
Implementierung aller möglicher Algorithmen und damit
berechenbarer Funktionen.
Der
Baukasten für Algorithmen wird vervollständigt, indem
primitiv rekursive Funktionen um einen Suchprozess, genannt
μ
- Rekursion, erweitert
werden:
Sei
wieder f ein gödelisiertes Problem der Art f: Nk
→ N.
M(f,
n
1
,…,n
k
,q)
:= {qϵN | f(n
1
,…,n
k
,q)=0
& für alle 0 <= p <= q: f(n
1
,…,n
k
,q)=
def.}
f(n1,…,nk,q)=0
kann als gödelisierte Form der Beschreibung einer zu suchenden
Problemlösung verstanden werden. M ist dann die Menge aller
Lösungen, die vom Startpunkt p = 0 durch Suche gefunden werden
können, da für alle 0 <= p <= q f definiert ist.
Die μ
- Rekursion bezeichnet nun
den Prozess, der zum Auffinden der ersten Lösung in M führt,
falls M nicht leer ist. Ist M leer, dann terminiert die μ -
Rekursion nicht !
μf(n
1
,…,n
k
)
:= min M(f,n
1
,…,n
k
),
falls M(f,n
1
,…,n
k
)
nicht leer, undefiniert sonst
Wie die
primitive Rekursion durch eine LOOP- Schleife, kann die μ
- Rekursion nun durch eine while
Schleife dargestellt werden: eine
while- Schleife wiederholt Anweisungen, solange eine Bedingung
erfüllt ist.
Beispiel:
Sei ein x ϵ N gegeben
und das kleinste y ϵ N
gesucht, das noch von x ganzzahlig geteilt werden kann. Dieses
Problem ist nicht primitiv rekursiv, jedoch μ -
Rekursiv. Mittels einer einfachen while- Schleife wird die Lösung
implementiert:
y := 0
while y mod y <> 0 Do
y := y + 1
END
1.3.5.3 λ
-
Kalkül und Funktionale Programmierung
Siehe
(Wikipedia:
Lambda Kalkül)
Das
Lambda- Kalkül ist ein von Alonso Church und Stephen Cole Kleene
1936 entwickelter und untersuchter Formalismus. Man kann ihn als
erste
funktionale
Programmiersprache
betrachten. Jedoch wurde er nicht als Programmiersprache, sondern als
Instrument zur Untersuchung von Berechenbarkeit und der
Formalisierung mathematischer Beweise.
Mit
dem Lambda Kalkül werden Ausdrücke gebildet und umgeformt,
die aus folgenden Grundbausteinen bestehen:
{a,
b, ….} = Menge der Variablen.
Variablen sind Kleinbuchstaben
λx.A
<=> Lambda - oder Funktionsabstraktion. Eine namenlose
(anonyme), einstellige Funktion. Diese bildet x gemäß der
durch Ausdruck A gegebenen Abbildungsvorschrift ab.
Beispiel:
λx.a bildet alle x auf eine Konstante a ab: f: x → a
Beispiel:
λx.λy.x bildet jedes x auf eine Funktion ab, die alle
y Abbilden auf das x abbilden: f: x → (g: y → x)
F
A <=> Funktionsanwendung / Applikation: Eine Funktion F wird
auf den Ausdruck A angewendet.
Beispiel:
λx.x t → t
Beispiel:
(λx.λy.x) t → λy.t
Beispiel:
λf.(f x) (λx.λy.x) t → (λx.λy.x)
→ λy.t
Das
war es ! Es gibt keine Grundrechenoperationen wie +/-, *, /, keine
logischen Operatoren oder Fallunterscheidungen. Der Lambda- Kalkül
ist sehr spartanisch. Trotzdem können alle "fehlenden"
Operationen und Strukturen der Programmierung aus ihm hergeleitet
werden.
Die
beiden Werte der binären Menge {true, false} können durch
zwei Lambda- Abstraktionen dargestellt werden:
λx.λy.x <=> true. Wende z.B. an auf t, f: λx.λy.x t f → λy.t f → t
λx.λy.y <=> false. Wende z.B. an auf t, f: λx.λy.y t f → λy.y f → f
1.3.5.4 Grenzen der Berechenbarkeit mit der
Turingmaschine erforschen
Ein gewissenhafter Programmierer könnte über
die von ihm eingesetzten Algorithmen Buch führen. Dabei weist er
jedem Algorithmus eine Nummer zu, wie Berechnung für
Schaltjahr: 1, Primzahltest: 2, ….
Wenden wir dieses System auf alle erdenklichen Algorithmen an, indem
wir eine Abbildung (Funktion) definieren wie folgt:
Num_A:
A → N, mit A <=> Menge aller Algorithmen und
N
<=> Menge der natürlichen Zahlen und
es
gilt: Wenn Ai
≠ Aj,
dann ist Num_A( Ai)
≠ Num_A(
Aj)
Num_A nummeriert
die Algorithmen durch. In der Mathematik wird dies als
Abzählung
bezeichnet. Dabei ist die Menge
aller Algorithmen unendlich, denn es können beliebig viele
sinnvolle und weniger sinnvolle, endliche, in Schritten gegliederte
Texte formuliert werden.
Auch die Menge aller
Turingmaschinen ist abzählbar und unendlich wie die der
Algorithmen.
Num_T:
T → N, mit T <=> Menge aller Turingmaschinen und
N
<=> Menge der natürlichen Zahlen und
es
gilt: Wenn Ti
≠ Tj,
dann ist Num_T( Ti)
≠ Num_T(
Tj)
Jede
Turingmaschine kann durch einen Algorithmus beschrieben werden, indem
eine Tabelle mit den Spalten
Zustand, Eingabe, Ausgabe,
Kopfbewegung, Folgezustand für
sie definiert wird. Damit kann z.B. die Nummer einer Turingmaschine i
(Num_T(Ti))
berechnet werden, indem wir ihr die Nummer des zugehörigen
Algorithmus geben:
Num_T(T
i
)
:= Num_A(A
i
)
wenn A
i
→
T
i
Wenn jede Turingmaschine
durch einen Algorithmus darstellbar ist, gilt dann auch die
Umkehrung: gibt es zu jedem Algorithmus eine Turingmaschine ? Oder
gibt es vielleicht Algorithmen, welche die einfache Turingmaschine
überfordern und einer komplexeren Konstruktion bedürfen ?
Alan Turing konnte zeigen, dass z.B. das Lambda-
Kalkül von Alonso Church die gleiche Menge von Algorithmen
abzubilden vermag wie seine Turing- Maschine. Bis heute konnte keine
Konstruktion für eine Rechenmaschine gefunden werden, die mehr
berechnen kann wie eine Turingmaschine. Es gilt damit nach wie vor
die von Turing und Church aufgestellte These:
Jeder Algorithmus kann durch
eine Turingmaschine dargestellt werden.
Anbei eine Turingmaschine, die zwei Dualzahlen
addiert. Ihr Zustandsautomat wurde aus dem Entscheidungsbaum für
den einstelligen Dualzahl Addierer der EVA- Funktion von oben
entwickelt. Bei jedem Zustandsübergang liest der Schreiblesekopf
den Wert vom aktuellen Platz auf dem Band ein (Kopfposition mit
Unterstrich markiert)
schreibt einen neuen Wert aufs Band zurück und bewegt den Kopf
um einen Platz nach rechts oder links. Wird der Zustand Halt
erreicht,
dann ist das Programm beendet. Die Herleitung aus dem
Entscheidungsbaum hat den Nachteil, das alle Stellen beider
Dualzahlen verschränkt aufs Band geschrienen werden müssen,
wie auch die Überträge. Die Turingmaschine kann aber so
erweitert werden, das separate Eingaben auf dem Band verschränkt
werden und nach der Addition wieder speariert.
Nur was kann man mit Algorithmen berechnen ? Gibt
es Dinge, die mit einem Algorithmus nicht berechnet werden können
? Auch diese Frage konnte Alan Turing mit einem Beispiel für
eine Aufgabenstellung beantworten, die prinzipiell nicht durch einen
Algorithmus lösbar ist: das Halteproblem.
Das Halteproblem stellt sich wie folgt: Gibt
es eine Turingmaschine, die als Eingabe einen Algorithmus und eine
Liste von Werten erwartet, die der Algorithmus verarbeiten soll, und
die eine 1 ausgibt, wenn die Abarbeitung des Algorithmus mit den
gegebenen Eingaben nach endlicher Zeit endet, und 0 wenn nicht ?
Die Existenz einer Turingmaschine, wie sie die
Lösung des Halteproblems fordert, führt zu logischen
Widersprüchen. Nehmen wir an, es gibt die Maschine, die das
Halteproblem löst. Sie sei formal als Funktion wie folgt
definiert:
Mit dieser Turingmaschine kann nun eine Funktion
Sonderbar konstruiert werden
wie folgt:
Sonderbar:
E → Sonderbar(E), wenn T_Halt(E,E) = 1, 1, sonst.
Wird mit
Sonderbar ein Text abgebildet, der als Algorithmus und Eingabe
interpretiert wird, wobei für diese Kombination T_Halt 1
lieferte, dann terminiert Sonderbar nicht (Endlosrekursion). Nun
bildet man mit Sonderbar den Algorithmus von Sonderbar selbst ab:
Würde T_Halt(Sonderbar, Sonderbar) = 1 sein, dann findet eine
Endlosrekursion statt - Widerspruch ! Liefert T_Halt(Sonderbar,
Sonderbar) = 0, was für diese Kombination nicht terminieren
bedeutet, dann terminiert die durch Sonderbar definierte Abbildung -
ebenfalls ein Widerspruch !
Das
Halteproblem zeigt, dass Funktionen formuliert werden können,
die prinzipiell nicht lösbar (nicht berechenbar) sind. Die Menge
aller Funktionen ist damit die Vereinigung der berechenbaren und der
nicht berechenbaren Funktionen. Die These von Church und Turing
umfasst auch folgende Aussage:
Jede berechenbare Funktion
kann durch einen Algorithmus dargestellt werden.
(Q: Wikipedia,
Church - Turing - These, Beweisskizze
Halteproblem)
1.3.5.5 Algorithmen steuern die Welt...
Algorithmen existieren nicht nur in der Welt der
Computer. In vielen hoch organisierten und ausdifferenzierten
Systemen ist der Begriff vom Algorithmus anwendbar.
So kann z.B. die Eiweißsynthese in den
Zellen als Algorithmus beschreiben werden. Dieser Algorithmus
erwartet dabei als Eingabe einen RNS- Strang (Molekülkette aus
Ribonukleinsäuren). Die Ausgabe sind Eiweiße, die dem
Stoffwechsel der Zellen dienen.
Weitere Beispiele:
1.4 Wie sich die Programmiersprachen entwickelten
Zur
Formulierung von Programmen für Computer wurden eine Vielzahl
von Programmiersprachen entwickelt. Die Sprachen sind gekennzeichnet
durch den Stand der Computertechnik zum Zeitpunkt ihrer Entwicklung.
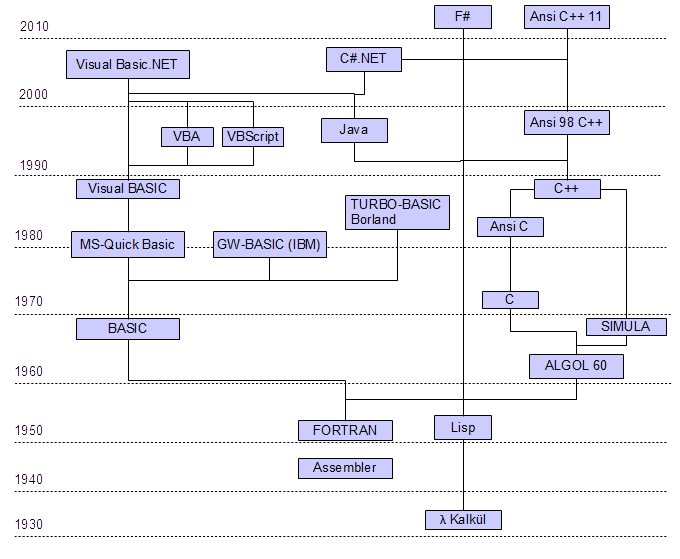
Man unterteilt die Programmiersprachen in folgende Generationen:
Generation:
Maschinensprachen sie sind spezifisch für jedes Computersystem,
die Schaltelemente der CPU werden direkt programmiert. Bsp:
0100.1100 1010.0011 ...
Generation:
Assemblersprachen die direkte Programmierung der Schaltelemente
durch 0 und 1 wird durch Operationskürzel wie ADD und MOV
ersetzt. Dadurch wird das Programm lesbarer. Die Assemblersprache
ist jedoch genauso wie die Maschinensprache an ein bestimmtes
Computersystem gebunden.
Bsp: MOV AX, [2000]; MOV BX,
[2002]; ADD AX, BX … → 0100.1100 1010.0011 ...
Generation:
höhere Programmiersprachen zwischen Computer und Programmierer
wird ein Compiler bzw. Interpreter geschaltet
(Übersetzungsprogramm). Die Programmiersprache kann Funktionen
mit komplexer Semantik für spezielle Aufgabengebiete enthalten
(z.B. Operatoren für Matrizen). Die Zwischenschicht
Compiler/Interpreter kann auf baulich verschiedenen Computersystemen
realisiert werden, so das die Programme portabel sind. Beispiele:
FORTRAN, LISP, C++, PL1, BASIC
Bsp: C = A + B; … → MOV
AX, [2000]; MOV BX, [2002]; ADD AX, BX … → 0100.1100
1010.0011 …
Objektorientierte
Programmiersprachen: Prozeduren und Daten werden zu Objekten
zusammengefasst. Z.B. kann der Auftrag zur Berechnung aller
Primzahlen in einem Intervall [a, b] durch ein Rechenauftrag-
Objekt dargestellt werden:
class
RechenauftragPrimzahlen { von; bis; berechne(); ergebnisliste[...]
}
A1 = new
RechenauftragPrimzahlen() { .von = 1, .bis = 100}
A1.berechne()
Ausgabe(A1.ergebnisliste)
Generation:
nicht prozedurale Programmiersprachen Compiler/Interpreter und
Anwendung verschmelzen, der Programmierer gibt der Anwendung
Aufträge, die Anwendung erzeugt intern Programme, welche die
Aufträge realisieren. Beispiel: SQL, Assistenten in MS Office97
Bsp: Select A + B as C From
TabDaten … → … C = A + B; … → MOV AX,
[2000]; MOV BX, [2002]; ADD AX, BX … → 0100.1100
1010.0011 ...
Generation:
Programmiersprachen der künstlichen Intelligenz- Interpreter
Systeme, mit denen Methoden der künstlichen Intelligenz einfach
realisierbar sind, bzw. Interaktion mit dem Computersystem in
natürlicher Sprache möglich ist. Beispiele: LSIP, PROLOG,
F#
1.5 Grundbegriffe der Programmierung
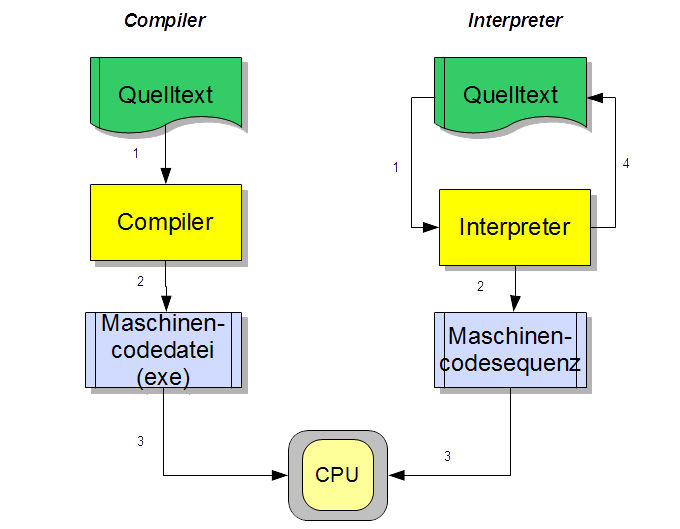
1.5.1 Compiler vs. Interpreter
Es gibt grundsätzlich zwei Arten der
Übersetzung eines Programms in einen ausführbaren
Maschinencode:
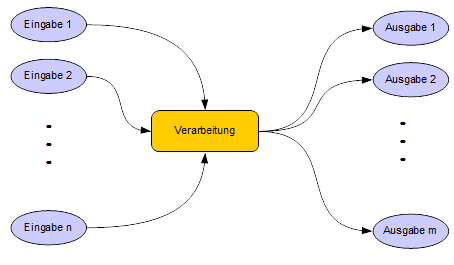
1.5.2 EVA- Prinzip
Im Zentrum steht die Berechnung einer Ausgabe aus
gegebenen Startwerten (Eingaben).
Ein Beispiel dafür ist die Umrechnung von
Polarkoordinaten (Drehwinkel + Abstand) in kartesische Koordinaten
(x,y). Das rotierende Flughafenradar erfasst z.B. die Position eines
Flugzeugs in Polarkoordinaten. Die umgerechnete y Koordinate
entspricht der Flughöhe.
Die
Ausgaben können wieder als Eingaben einer weiteren
Verarbeitungsstufe dienen. Es
entstehen komplexe Verarbeitungsnetze.
Eine Verarbeitungsstufe wird auch als Prozedur
bezeichnet. In den ersten
Jahrzehnten der EDV bildeten im Wesentlichen Prozeduren die
Programmstruktur. Man spricht auch von der rein prozeduralen
Programmierung.
Das EVA- Prinzip kann auf verschiedene Art und
Weise implementiert (umgesetzt) werden:
1.5.3 Schrittweise Verfeinerung
Die Schrittweise Verfeinerung ist
Vorgehensweise oder auch Strategie, zur Lösung komplexer
Probleme. Dabei wird ein komplexes Problem in eine Menge voneinander
isolierter Teilprobleme aufgelöst. Gibt es für ein
Teilproblem eine bekannte Lösung, dann wird das Teilproblem
durch diese ersetzt.
Gibt es keine bekannte Lösung, dann ist das
Teilproblem wiederum in voneinander isolierte Teilprobleme
aufzuteilen, und die Liste von Teilproblemen erneut auf eventuell
bekannte Lösungen zu untersuchen.
1.5.4 Funktionale Programmierung
Prozeduren können durch Funktionen
implementiert werden.
Eine Funktion bildet eine Liste von Eingangswerten
aus einen Ausgangswert ab:
E1 --+
|
Eingänge E2 --+-Funktion_f-> Ausgangswert
… |
En --+
Beispiel:
Kreisumfang(D) => π * D
wobei:
D - Argument/Eingabe
=> π * D - Verarbeitung
Kreisumfang(D) - Ausgabe
Bsp.:
10 -+
|
Kreisumfang(10) => π * 10
---+---
|
31,4 <----+
D wird ersetzt durch 10, der Funktionswert
errechnet und mit diesem der Aufruf (Kreisumfang(10))
ersetzt
Die funktionale Programmierung
beschränkt sich auf dieses einfache Ersetzungsprinzip:
Eingangswerte durch einen Ausgangswert ersetzen. Erstaunlicherweise
ist das ausreichend, um Lösungen für alle berechenbaren
Probleme hinreichend genau auszudrücken. Programmiersprachen wie
Lisp oder F#
sind Beispiele.
1.5.5 Imperative Programmierung
Digitale Rechenmaschinen werden durch Befehle
gesteuert. Dieses Prinzip wird in der imperative Programmierung
verallgemeinert, indem Prozeduren durch Befehlsfolgen implementiert
werden, die an eine abstrakte Maschine gerichtet sind.
Beispiel einer solchen abstrakten Maschine sind
die Turingmaschine
oder der von
Neumann Rechner.
Fast jeder reale Computer ist bis heute ein von
Neumann Rechner.
Das folgende Bild zeigt einen Universalrechner,
der Elemente der Turingmaschine (Bänder als Speicher, Schreib-
Leseköpfe) und des von Neumann- Rechners (Rechen- und
Steuerwerk) vereint.
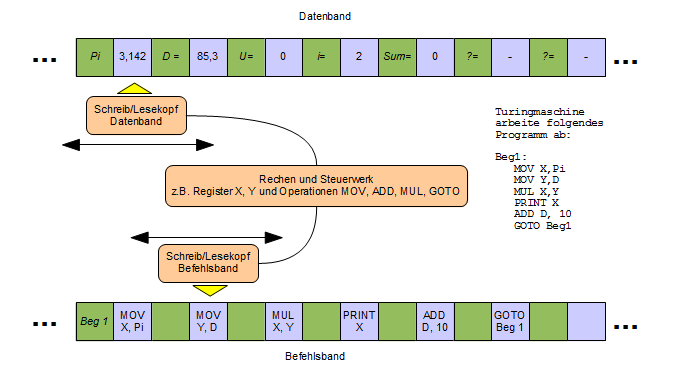
Die
Bänder sind in Zellen unterteilt. Jede Zelle hat eine Adresse
(symbolisch). Z.B. ist auf dem Datenband mit der Adresse Pi
die Speicherzelle definiert, welche
den Wert 3,142 speichert. Auf dem Befehlsband ist mit der Adresse Beg
1 der Einsprungpunkt (=
Startpunkt) in ein Programm definiert.
Mittels
Schreib/Leseköpfe kann ein Rechen- und Steuerwerk
Befehle und Daten von den Bändern
einlesen, und zurückschreiben.
Das Rechen- und
Steuerwerk arbeite im wesentlichen Befehle ab, die es einen nach dem
anderen vom Befehlsband einliest. Bei der Verarbeitung eines Befehls
werden mittels des Schreib- Lesekopfes vom Datenband Daten eingelesen
oder auf dieses geschrieben. Im Bild wird ein kleines Programm zur
Berechnung des Kreisumfanges für einen gegeben Radius
abgearbeitet mit den folgenden Schritten:
lese Durchmesser in Register A ein
lade Pi in Register B
multipliziere Register A mit Register B
gebe Ergebnis aus
1.5.6 Kommunizierende Objekte - das Paradigma der
objektorientierten Programmierung
Die objektorientierte Programmierung ist eine
Erweiterung der klassischen, prozeduralen Programmierung um
Entwurfsmethoden und Ausdrucksmittel, durch welche
die Abbildung von Geschäftsprozessen auf
Programmstrukturen vereinfacht,
und der Programmcode transparenter wird.
Die Welt besteht aus Objekten, die miteinander
kommunizieren. Die Kommunikation erfolgt über Nachrichten,
welche die Objekte untereinander austauschen.
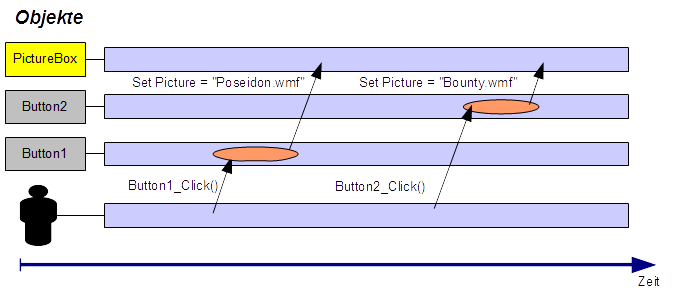
Aus prozeduraler Sicht sind Nachrichten
Prozeduren, die an Objekte gebunden sind.
1.5.7 Entwicklungszyklus
Die Entwicklung eines Computerprogramms erfolgt in
mehreren Phasen:
Spezifikation:
Was soll das Programm leisten? Welche
Rechenleistung/Speicherkapazität wird benötigt? Welche
Peripherie wird benötigt? Ist das Projekt wirtschaftlich
realisierbar
Entwurf:
Die komplexe Aufgabe wird in Teilaufgaben zerlegt. Lösungsweg
der Teilaufgaben wird informell (Pseudocode) beschrieben.
Codierung/Implementierung:
Alle informellen Beschreibung werden in eine vom Computersystem
unterstützten Programmiersprache überführt.
Kompilierung:
Die Programmtexte werden mittels eines Übersetzungsprogramms
(Compiler) in die Maschinensprache übersetzt. Werden vom
Compiler Syntaxfehler entdeckt, dann sind diese vom Programmierer zu
analysieren und zu beheben.
Linken:
Alle einzeln übersetzten Programmfragmente werden zu einem
großen Programmmodul montiert (.EXE- Datei)
Testphase
(alpha- Stadium): Verschiedene Einsatzszenarien werden
mit dem Programm durchgeführt. Es wird beobachtet, ob das
Programm korrekt funktioniert. Treten Fehlfunktionen auf, sind ihre
Ursachen einzugrenzen, und es muss in Phase 2 zurückgesprungen
werden.
Auslieferung
zum Beta- Test: Das Programm wird unter dem Vorbehalt des
nicht störungsfreien Betriebs an eine Auswahl qualifizierter
Anwender ausgeliefert, die es unter realen Bedingungen einsetzen.
Fehlfunktionen werden von den Anwendern dem Entwicklerteam
mitgeteilt.
Golden-Code:
Nach Tilgung aller im Betatest aufgetretener Fehler wird die finale
Version erzeugt und freigegeben. Das Programm wird jetzt an alle
Anwender ausgeliefert.
1.6 Programmentwicklung am Beispiel: Suche alle
Primzahlen in einem Intervall [a, b]
An einem Beispiel sollen die Grundlagen der
Programmierung erläutert werden. Dabei wird der Weg von der
Formulierung des Problems bis zum Aufstellen der Lösung
dargestellt.
Primzahlen sind ganze Zahlen, die nur durch 1 und
durch sich selbst ganzzahlig teilbar sind. Beispiele:
2, 3, 5, 7, 11, 13
Keine Primzahl ist z.B. 39, da neben 1 und 39 auch
3 ein ganzzahliger Teiler ist:
39 : 3 = 13
Die Aufgabe besteht im Finden aller Primzahlen Pn
aus einem Intervall [a, b]. Z.B.:
Pn aus [10, 20]: 11, 13, 17,
19
1.6.1 Lösung
Bei der Lösung werden zwei grundlegende
Techniken wechselseitig angewendet:
Modularisierung:
Die Gesamtaufgabe wird in voneinander isolierte Teilaufgaben zerlegt
Schrittweise
Verfeinerung:
Jede Teilaufgabe wird modularisiert, solange keine elementare Lösung
für diese bekannt ist
Die
Aufgabe "Suche Primzahlen in einem Intervall [a, b]" kann
in folgende Teilaufgaben (Modularisierung) zerlegt werden:
Prüfen, ob eine gegebene Zahl z Primzahl ist
Bereitstellen jeder Zahl aus dem Intervall [a, b] für einen
Primzahltest
1.6.1.1 Teilaufgabe 1:
Primzahltest
Teilaufgabe 1 kann wiederum heruntergebrochen
werden in eine Folge von Einzelprüfungen auf Teilbarkeit.
Folgender Datenflussgraph visualisiert das:
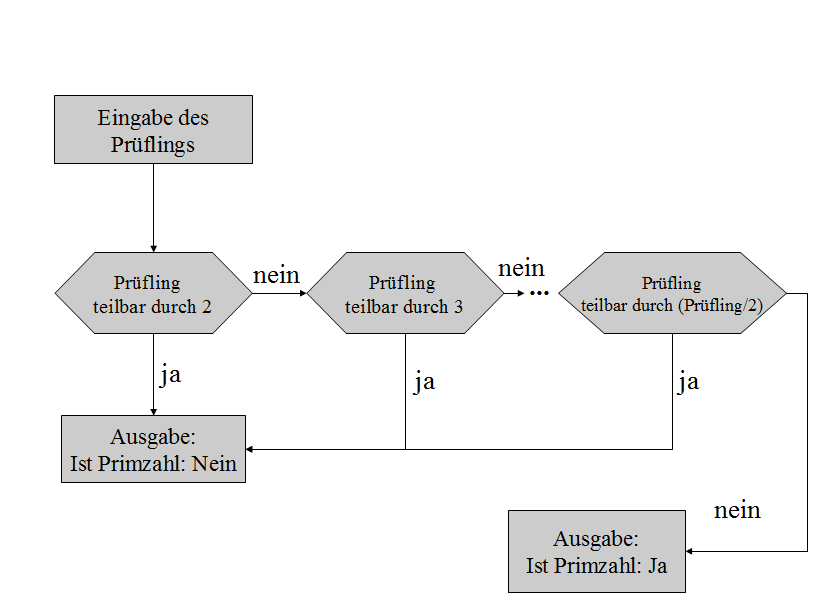
1.6.1.2 Teilaufgabe 2: Bereitstellen
jeder Zahl aus dem Intervall [a, b] für einen Primzahltest
Auch die Teilaufgabe 2 wird in eine Folge
elementarer Befehle heruntergebrochen, wie im folgenden Struktogramm
dargestellt:
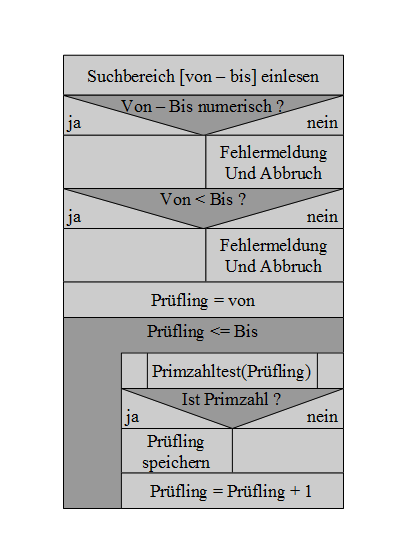
1.6.1.3 Primzahlscanner
funktional codieren
Teilaufgabe
1 kann z.B. durch folgende Funktion dargestellt werden (Pseudokode):
IstPrimzahl(z): z → z Mod 2 <> 0 AND TesteWeiterAufPrimzahl(z, 3)
TesteWeiterAufPrimzahl(z, t): z,t → z Mod t <> 0 AND
Wenn t = z/2
dann true
sonst TesteWeiterAufPrimzahl(z, t + 1)
Die
funktionale Lösung ist eine, dem Mathematiker geläufige
Form und besticht durch ihre Kürze. Nicht- Mathematikern haben
aber in der Regel große Probleme, die Wirkung dieser
funktionalen Ausdrücke, die auf Rekursion beruht, zu verstehen.
Auch
für Teilaufgabe 2 gibt es eine Funktionale Lösung
(Pseudokode):
AllePrimzahlenIn(a, b): a, b → Alle x in [a, b] für die gilt: IstPrimzahl(x)
Die Funktion bildet dabei das Paar a,b auf eine Menge mit allen
Primzahlen zwischen a und b ab.
1.7 Allgemeine Strukturen von Programmiersprachen
1.7.1 Blöcke
Die elementarste Struktur aller
Programmiersprachen sind Blöcke. Ein Block ist ein
zusammenhängendes Stück Text (Programmcode), das durch
spezielle Schlüsselworte abgegrenzt wird.
Blockbeginn Schlüsselwort
Programmtext
Blockende Schlüsselwort
Im Folgenden einige
Blöcke, die quasi jede Programmiersprache aufweist:
|
Schlüsselwörter
|
Bezeichnung
|
|
Prog <Programmname>
Module
End Prog
|
Programmblock:
Umfasst das komplette Programm.
|
|
// C, C++, C#, JavaScript
/*
Komentartext
*/
|
Kommentarblock
|
|
' VB
Sub
<Name>(Parameterliste)
'Implmentierung
...
End Sub
// C#
void
<Name>(Parameterliste) {
//
Implementierung …
}
// JavaScript
Function <Name>
(Parameterliste) {
//
Implementierung …
}
|
Unterprogrammblock: Schließt
Liste von Anweisungen ein, die über einen Namen geladen und
ausgeführt werden können
|
|
' VB
Function
<Name>(Parameterliste) as <Typ>
return
<Funktionswert berechnen>
End Function
// C, C++, C#
<Typ>
<Name>(Parameterliste) {
return
<Funktionswert berechnen>;
}
// JavaScript
Function <Name>
(Parameterliste) {
return
<Funktionswert berechnen>;
}
;; LISP
(defun <Name>
(Parameterliste) (<Expr>))
|
Funktionsblock
|
|
' VB
IF <Bedingung> Then
<Anweisungen...>
End IF
// C, C++, C#, JavaScript
if(<Bedingung>) {
<Anweisungen...>
}
;; LISP
(cond <Bedinung>
<Expr_if_true> <Expr_if_false>)
|
Bedingter Anweisungsblock:
Schließt Liste von Anweisungen ein, die nur ausgeführt
werden, wenn die Bedingung erfüllt ist.
|
|
' VB
Wihle <Bedingung>
<Anweisungsliste>
Wend
// C, C++, C#, JavaScript
while(<Bedingung>)
{
<Anweisungsliste>
}
|
Schleifenblock: Anweislungsliste
wird sooft wiederholt, solange die Bedingung gilt.
|
1.7.1.1 Verschachtlung
Die Anweisungslisten innerhalb von Blöcken
können wieder in Blöcke eingeschlossen werden, so dass eine
Baumstruktur entsteht. Man spricht von Verschachtlung.
|
Allgemein
|
Beispiel
|
|
Beginn Block1
'
Anweisungen
...
Beginn
Block2
'
Anweisungen
...
End
Block2
'
Anweisungen
...
End Block1
|
Sub Hauptprogramm
A
= 5
B
= 4
IF
A > B Then
Debug.Print
"A ist größer als B"
End
IF
End Sub
|
1.7.1.2 LISP- Blöcke als Programmiersprache
LISP
ist eine der ältesten Programmiersprachen. Bezüglich der
Syntax kann sie als minimal bezeichnet werden, denn sie besteht im
wesentlichen nur aus dem Block, den man in LISP Liste nennt.
Eine Liste wird in LISP
in runden Klammern eingeschlossen:
( < Block/ Listeninhalt> )
Der Listeninhalt ist eine
Aufzählung von Konstanten und Bezeichnern (hier A, B, C), die
durch Leerzeichen getrennt werden:
(A B C … )
Einfache Operationen wie eine
Addition der drei Werten 7, 11 und 13 wird durch eine Liste
dargestellt:
(+ 7 11 13)
Ein Term, der sich aus Addition
und Multiplikation zusammensetzt, entsteht aus zwei Listen, die
verschachtelt werden:
(* 2 (+ 7 11 13))
Einen bedingten Anweisungsblock,
der einen Wert berechnet, wenn eine Bedingung erfüllt ist,
entsteht aus drei verschachtelten Listen:
(cond
(= b 0) (+ a 1))
Ein
Unterprogrammblock hat als erstes Listenelement das Schlüsselwort
define
:
(define (gcd a b) (cond (= b 0) (a) (gcd b (remainder a b))))
---+---- ---+-- -+- + -----+-------
+> Progname +>Bed.| | +> UP, das den Rest der ganzzahligen
von UP | | Division von a und b berechnet
| | ------+--------
| | +> 2. Parameter
| +> 1. Parameter
| -----------+-----------
| +> Block, wenn if Bed. false
+> Block, wenn if Bed. true
Das Unterprogramm ist eine
Rekursive Funktion, die den euklidischen Algorithmus zur Berechnung
des größten gemeinsamen Teilers zweier ganzer Zahlen
implementiert.
Diese
spartanische Syntax mag primitiv erscheinen - LISP ist jedoch ein
sehr Leistungsfähiges Werkzeug. In den 1980-er Jahren war LISP
die Sprache der
Künstlichen
Intelligenz.
Gerade
durch diese einfache Syntax kann ein Programmierer leicht Programme
schreiben, die selber LISP- Programme generieren. Hierdurch kann sehr
einfach eine komplexe Symbolverarbeitung realisiert werden !
1.7.2 Literale
Literale gehören zu den Grundbausteinen einer
Programmiersprache und bezeichnen die Vereinigung der Mengen aller
1.7.3 Operatoren
Operatoren sind grundlegende Abbildungen von
Mengen in sich selbst. Beispielsweise ist die Addition zweier
Festkommazahlen ein Operator.
Eine Anweisung kann mehrere Operatoren enthalten
wie:
A = 3 * (B + 99)
In diesem Falle muss bei der Ausführung der Anweisung über
die Reihenfolge entschieden werden, in der die Operatoren anzuwenden
sind. Basis dafür ist die Priorität der Operatoren.
Operatoren mit höherer Priorität werden vor Operatoren mit
niedrigerer Priorität ausgeführt.
1.7.4 Datentypen
1.7.5 Anweisungen
Eine Anweisung ist ein ausführbarer Befehl.
Befehle können elementar oder komplex sein.
Elementare Befehle sind direkt ausführbar wie
z.B. einfache Sprungbefehle:
Goto SPRUNGMARKE
Komplexe Befehle setzen sich aus Speicherzugriffsbefehlen,
Operationen und Zuweisungen zusammen.
A := 3 * (B + 99)
1.7.5.1 Kommentar - Anweisung
Jede Programmiersprache enthält eine
Kommentar - Anweisung. Diese schließt Text von der Übersetzung
aus. Dies kann man nutzen, um bei der Entwicklung temporär Code
abzuschalten oder Anmerkungen in den Programmkode einzufügen. Im
Folgenden einige Einsatzbeispiele für Kommentare:
' Eine Kommentarzeile
' Eine temporär abgeschaltete Anweisung (auskommentieren)
' A = 3 * B
B = 5 * C ' Ein Kommentar im Anschluss an eine Anweisung
1.7.5.2 Bindung
Bindungen definieren Ersatzsymbole für Werte
oder Funktionen. So ist z.B. der Buchstabe π
in der Mathematik an die
Zahlenfolge 3,142... gebunden.
π ← 3, 142
Bindungsanweisungen sind
Bestandteil von imperativen (= Konstanten Deklarationen) und
funktionalen Sprachen.
1.7.5.3 Variablendeklarationen
Variablen sind benannte Speicherplätze.
In die Speicherplätze wird geschrieben oder aus ihnen wird
gelesen, indem auf diese der Zuweisungsoperator := mit einem Wert
angewendet wird:
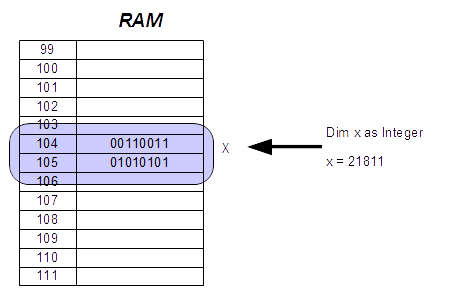
Variablen
sind Bestandteile von imperativen Programmiersprachen, jedoch nicht
von funktionalen.
' Speichern des Wertes 3.14 in meineVariable
meineVariable = 3.14
' Lesen eines Wertes aus meinerVariable und speichern in deinerVariable
deineVariable = meineVariable
1.7.5.4 Zuweisung
Eine Zuweisung ist eine spezielle Anweisung einer
imperativen Programmiersprache der Form:
Variable := Wert
Sie entspricht einem Kopierbefehl, wobei der evaluierte Wert rechts
neben dem Gleichheitszeichen an den benannten Speicherplatz
(Variable) links neben den Gleichheitszeichen kopiert.
1.7.6 Funktionen
Eine Funktion bildet eine Liste von Eingangswerten
aus einen Ausgangswert ab:
E1 --+
|
Eingänge E2 --+-Funktion_f-> Ausgangswert
… |
En --+
Ein funktionale Abbildung wird in
einer Programmiersprache durch eine spezielle Anweisung durchgeführt,
genannt Funktionsaufruf:
Ausgangswert = Funktion_f (E1, E1, …, En)
| | |_____________|
| | |
Funktions- Funktions- Parameterliste
wert name
1.7.6.1 Bedingte Ausdrücke
Ein bedingter
Ausdruck ist eine spezielle Funktion mit drei Parametern:
' VB
Ergebnis = IIF(<Bedingung>, <ExprA>, <ExprB>)
// C, C++, C#
Ergebnis = <Bdingung> ? <ExprA> : <ExprB>;
Zuerst wird die Bedingung evaluiert. Ergibt sie den Wert true,
dann wird ExprA evaluiert und deren Wert entspricht dem Ausgangswert.
Sonst entspricht der Evaluierte Wert von ExprB dem Ausganswert.
1.7.6.2 Lambda-
Ausdrücke
Der
Begriff Lambda Ausdruck wurde in einem Formalismus der Mathematiker
Alonzo Church und Stephe Kleene in den 1930 Jahren geprägt
(Lambda
Kalkül
). Dieser Kalkül wird auch
als der Urahn der funktionalen Programmierung betrachtet.
Ein Lambda- Ausdruck ist eine eine unbenannte
Abbildungsvorschrift. Hier werden solche Abbildungsvorschriften mit
dem griechischen Buchstaben λ
gekennzeichnet:
λ
:
(x1,...,xn) → (y1, …., ym)
' VB
Function(x1, … , xn) <Expr>
// C#
(x1, … , xn) => <Expr>
1.8 Objektorientierte Programmierung
Die objektorientierte Programmierung ist eine
Erweiterung der klassischen, prozeduralen Programmierung um
Entwurfsmethoden und Ausdrucksmittel, durch welche
die Abbildung von Geschäftsprozessen auf
Programmstrukturen vereinfacht,
und der Programmcode transparenter wird.
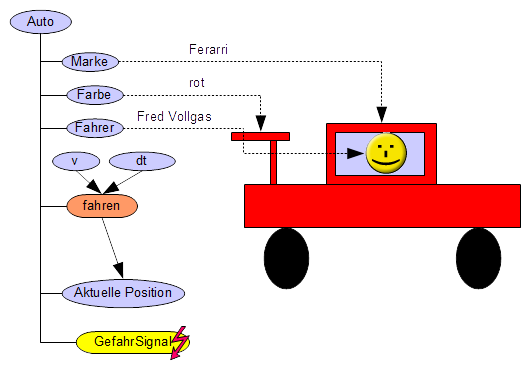
Von zentraler Bedeutung sind dabei Objekte:
|
Definition
|
Objekt
|
Ein Objekt steht für ein konkretes Ding (z.B. Der rote
Ferrari von Fred Vollgas oder die Tabelle 1 im
Arbeitsblatt Umsätze).
Objekte besitzen einen inneren Zustand. Z.B. hat der rote
Ferrari von Fred Vollgas eine Geschwindigkeit, und die Zelle $A1
in Tabelle 1 des Wert 99. Der Zugriff auf den inneren Zustand
erfolgt über Eigenschaften.
Objekte kann man beeinflussen, indem man ihnen Nachrichten
sendet. Z.B. kann man den roten Ferrari in einer Simulation
auffordern, die Geschwindigkeit auf 100 km/h zu reduzieren, oder
dem Tabellenblatt mitteilen, den Hintergrund der Zelle $A1 rot zu
färben.
Zustandsänderungen in Objekten können Ereignisse
auslösen. Schert vor dem Ferrari urplötzlich aus der
rechten Spur eine grüne Ente aus, die den linken
Fahrstreifen mit Tempo 100 km/h blockiert, dann wird der Ferrari-
Fahrer wütend, und hupt (= löst das Ereignis Hupen)
aus. Durch dieses Ereignis können wiederum eine Reihe von
Nachrichten erzeugt werden, die an die umgebenden Objekte
gesendet werden (z.B. Nachricht Hupsignal an die grüne Ente
gerichtet).
|
1.8.1 Graphische Darstellung von Objekten mittels
Objektdiagramm
Die objektorientierte Sichtweise erleichtert die
die notwendige Formalisierung von Aufgaben- Problemstellungen bei der
Softwareentwicklung, indem sie eine 1:1 Abbildung der Realität
auf den Entwurf ermöglicht. 1:1 bedeutet nicht, das alle Details
der Realität im Entwurf nachgebildet werden. Der Entwurf
abstrahiert nach wie vor von der Realität, indem er die
Abbildung auf die für die Aufgabenstellung wesentlichen
Eigenschaften und Prozesse einschränkt. Jedoch ist weniger
Abstraktion notwendig als bei der rein Prozeduralen Programmierung,
da diese zusätzlich erfordert, alle Objekte in Mengen aus Daten
und diese manipulierende Prozeduren aufzulösen.
|
Objektdiagramm
|
Objekt
|
|
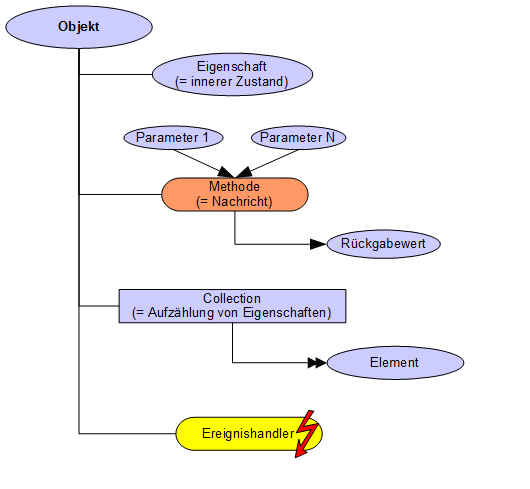
alternativ:
Objekt
|
+-
Eigenschaft
|
+-
M: Methode(Param1, Param2)
|
+-
C: Collection
|
+-
E: Event
|
|
1.8.2 Beispiel: Klasse Stoppuhr
Als Beispiel für eine Klassendeklaration und
Objekte diene die Klasse Stoppuhr.
Mit einem Stoppuhr- Objekt kann in einem Programm die Rechenzeit für
aufwendige Berechnungen gemessen werden.

1.8.3 Innerer Zustand
Objekte können wie Variablen Informationen
speichern. Dieser objekt- interne Informationsspeicher wird als
Innerer Zustand bezeichnet.
Der direkte Zugriff auf
den inneren Zustand ist in der Regel unzulässig. Beeinflusst
werden kann der innere Zustand nur durch Nachrichten, die das Objekt
empfängt.
1.8.4 Methoden
Aus der Perspektive der
Objektorientierung sind Methoden Nachrichten, die an ein Objekt
gesendet werden. Diese Nachrichten beeinflussen den inneren Zustand
eines Objektes. Viele Programmiersprachen implementieren Methoden
durch Unterprogramme, die Zugriff auf den inneren Zustand eines
Objekts haben.
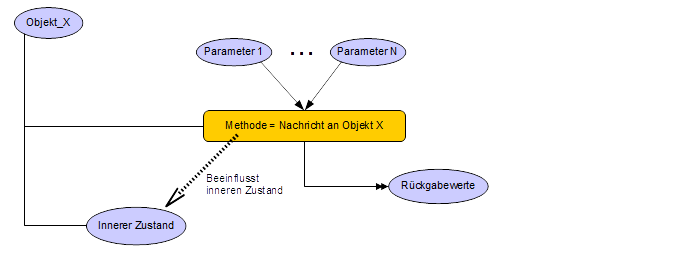
1.8.5 Eigenschaften
Eigenschaften sind die Schnittstellen zum inneren
Zustand eines Objektes.
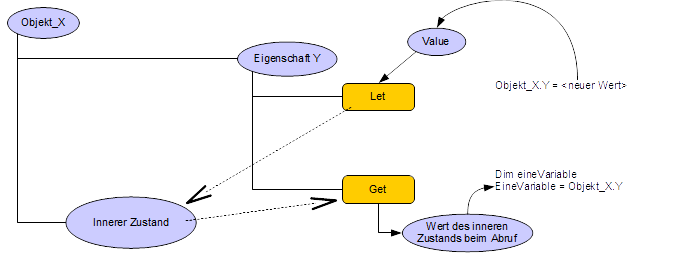
1.8.6 Ereignisse
Wenn ein Objekt einen
besonderen Zustand annimmt, kann es abhängig von der
Aufgabenstellung erforderlich sein, andere Objekte darüber zu
informieren. Diese Situation wird Ereignis genannt.
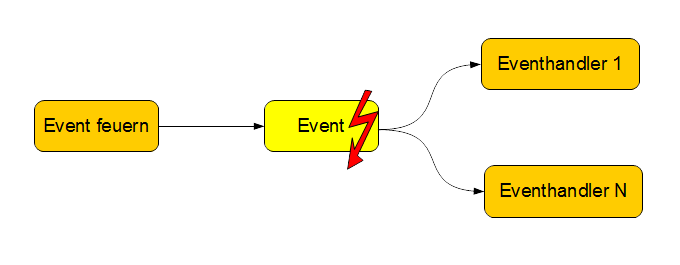
Ein
"Ereignis feuern" kann man sich wie einen Methodenaufruf
vorstellen. Jedoch ist die Methode nicht fest beim Implementieren
definiert worden. Stattdessen können während der Laufzeit
Methode an Ereignisse "gebunden" werden. Diese an ein
Ereignis gebundenen Methoden werden auch Eventhandler genannt.
1.8.7 Primzahlscanner objektorientiert implementieren
Teilaufgabe 1 wird durch Zahlenobjekte gelöst,
die eine IstPrimzahl- Methode besitzen. Wir senden bildlich
gesprochen dem Zahlenobjekt eine Anfrage, ob es eine Primzahl ist
oder nicht, indem wir seine IstPrimzahl- Methode aufrufen. Gibt diese
true zurück, dann ist das Zahlenobjekt eine Primzahl, sonst
nicht.

Teilaufgabe
2 wird durch zwei Objekte gelöst. Das eine (Zahlenbereich)
erzeugt für vorgegebene Grenzen eine Liste aus Zahlenobjekten,
die alle Zahlen innerhalb der Grenzen als Zahlenobjekte umfasst.
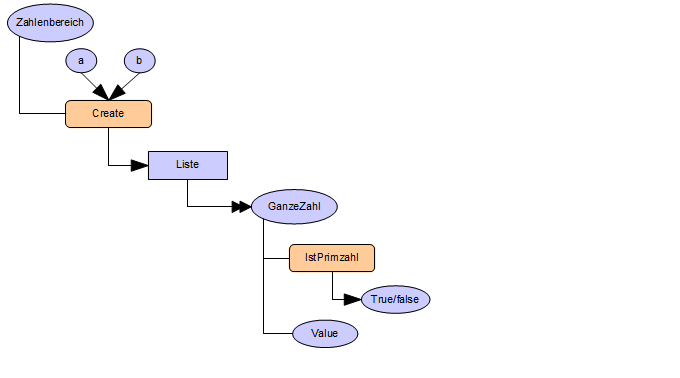
Das andere (Primzahlscanner) filtert die Liste,
indem es jeden Eintrag über die IstPrimzahl- Methode befragt, ob
es eine Primzahl ist. Objekte von Primzahlen werden in die
Ergebnisliste kopiert
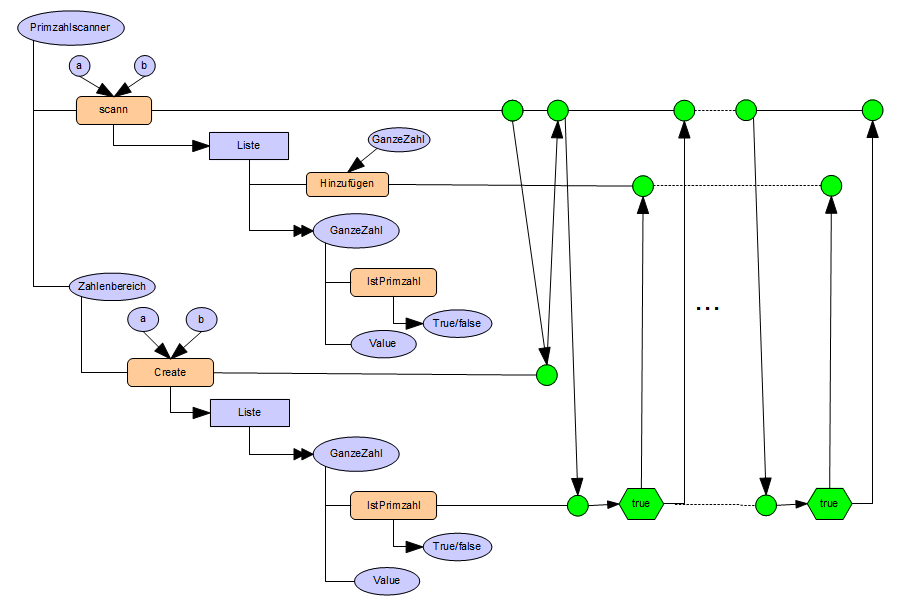
1.9 Datenorientierte
Programmierung
In
der Datenorientierten Programmierung oder Sicht stehen die permanent
gespeicherten Daten im Mittelpunkt. Diese bilden wesentliche
Geschäftsprozesse ab, weshalb sie dauerhaft gespeichert werden,
und sind damit für Unternehmen von besonderer Bedeutung.
Die
Trennung von Datenspeicherung und Datenverarbeitung erfolgte schon in
den 1970-er Jahren mit dem Aufkommen der ersten relationalen
Datenbankserver. Diese speichern Daten in Tabellensystemen,
Relationen
genannt.
1.9.1 Datenbankmodellierung
mit EF- Diagrammen
Für
die Modellierung von Datenbanken wurden eigene Diagramme entwickelt.
Der Prototyp sind die von P. Chen 1976 vorgestellten Entity-
Relationship- Diagramme. Im Folgenden die Modellierung einer
Datenbank für die Artikelverwaltung in einem Lager mittels ER-
Diagramm:
1.9.2 SQL
Mit
den relationalen Datenbankservern etablierte sich eine
standardisierte Schnittstelle für den Zugriff und die Verwaltung
von Daten:
SQL
= Structured Query Language
.
Im
Folgenden ein Auszug aus SQL
|
Pos
|
SQL Befehl, Beispiel
|
Bedeutung
|
|
1
|
create table termine (
zeit
datetime,
thema
varchar
)
|
Erzeugt auf dem Datenbankserver eine Tabelle
mit den beiden Spalten zeit,
und thema.
|
|
2
|
insert into termine
values
('3/9/2003 19:00',
'Zahnartzt')
go
|
Fügt in die Tabelle Termine einen
neuen Datensatz ein.
|
|
3
|
Select * from termine
where zeit between '3/1/2003 00:00' and '3/31/2003 23:59'
|
Listet alle Datensätze aus der Tabelle
Termine auf, die für den Monat März im Jahr 2003 gelten.
|
|
4
|
delete from termine where
zeit between '3/9/2003 00:00' and '3/9/2003 23:59'
|
Löscht alle Termine am 9.3.2003
|
|
5
|
Update termine set zeit =
'3/9/2003 17:00' where zeit = '3/9/2003 19:00'
|
Verlegt den Zahnarzttermin vom 9.3.2003 von
19:00 auf 17:00 Uhr
|
1.10 Dokument-orientierte
Programmierung
1.10.1 HTML
1.10.2 XML
http://mkoit/woc.aspx?path=Wissen.programmieren.xml
1.10.3 DOM
1.10.3.1 Serverseitiger
Zugriff auf DOM mittels System.XML.XmlDocument
1.10.3.2 Clientseitiger
Zugriff mittels JavaScript jQuery
1.10.3.3 Clientseitiger
Zugriff mittels XSLT
http://mkoit/woc.aspx?path=Wissen.programmieren.xml